Optimierungsfunktionen in der Portfoliotheorie
Optimierungsfunktionen werden in der Finanzportfolioverwaltung oft im Rahmen der Portfoliotheorie genutzt. Optimierungsfunktionen werden dabei meist durch Lagrange-Funktionen L dargestellt, die neben den Minimierungsfunktionen auch die Gleichungsnebenbedingungen und Ungleichungsnebenbedingungen enthalten. Die Optimierungsfunktionen sind in der theoretischen Behandlung von Portfoliozusammensetzungen in der Regel abhängig vom Gewichtsvektor
w‚ = (w1, w2, …, wn),
d. h. es gilt L = L(w).
Zweck der Optimierungsfunktionen ist die nach bestimmten Kriterien optimale Zusammensetzung w* des Zielportfolios zu ermitteln. Das Optimalitätskriterium ist dabei das Minimum der Optimierungsfunktion, d. h. die Berechnung desjenigen w* für das gilt:
L(w*) = min L(w)
Die Modellierung konkreter Problemstellungen in der Form von entsprechenden Optimierungsfunktionen ist adhoc nicht in einem standardisierten Verfahren möglich. Insbesondere die Auswahl der Gleichungsnebenbedingungen sowie Ungleichungsnebenbedingungen und die Abschätzung der Wirkung dieser auf das Ergebnis sind bei komplexen Optimierungsfunktionen anspruchsvoll. Nur in wenigen Fällen gelingt es, eine analytische Lösung vorzulegen. In der Regel sind die Optimierungsfunktionen nicht geschlossen lösbar und es müssen numerische Verfahren zur Suche des Minimums der Optimierungsfunktion angewendet werden.
Konkrete Optimierungsfunktionen mit Gleichungsnebenbedingungen
Beispiele für Lagrange-Funktionen in der Portfoliotheorie, die als Optimierungsfunktionen dienen:
Minimum-Varianz-Portfolio
L = w’Cw + λ1*(1 – w‘1)
Effizienzlinie nach Markowitz (Variante I)
L = w’Cw + λ1*(1 – w‘1) + λ2*(R – w‘r)
Effizienzlinie nach Markowitz (Variante II)
L = –w‘r + λ1*(1 – w‘1) + λ2*(S² – w’Cw)
Minimierung des Tracking-Error bei vorgegebener Renditeabweichung
L = (w‘–W‘)C(w-W) + λ1*(0 – (w‘-W‘)1) + λ2*(ΔR – (w‘-W‘)r)
Effizienzlinie nach Markowitz bei vorgegebenem Tracking-Error
L = w’Cw + λ1*(1 – w‘1) + λ2*(R – w‘r) + λ3*(TE² – (w‘-W‘)C(w-W))
Minimierung der Varianz bei variablem Tracking-Error
L = w’Cw + λ1*(1 – w‘1) + λ3*(TE² – (w‘-W‘)C(w-W))
Minimierung der Varianz bei variablem Umschichtungsvolumen
L = w’Cw + λ1*(1 – w‘1) + λ4*(U² – K(w‘-W‘)E(w-W))
Renditemaximierung bei fester Varianz und variablem Umschichtungsvolumen
L = –w’r + λ1*(1 – w‘1) + λ4*(U² – K(w‘-W‘)E(w-W)) + λ5*(S² – w’Cw)
Verschiedene Minimierungsfunktionen sind hier über ein oder mehrere Lagrange-Parameter λ mit Gleichungsnebenbedingungen zur finalen Optimierungsfunktionen L(w) verbunden. Als Minimierungsfunktionen werden z. B. verwendet: Portfolio Varianz w’Cw, Portfolio Tracking-Error gegen Benchmark (w‘-W‘)C(w-W) oder negative Portfolio Rendite –w’r. Mit C ist die n×n dimensionale Kovarianzmatrix bezeichnet, W ist die Zusammensetzung einer vorgegebenen Benchmark und r‘ = (r1, r2, …, rn) ist der n-dimensionale Vektor der Ertragserwartungen der einzelnen im Anlageuniversum befindlichen Vermögenswerte. Weiter bezeichnet R die feste oder variable aber vorgegebene Portfoliorendite, S² die feste oder variable aber vorgegebene Portfoliovarianz, TE² den festen oder variablen aber vorgegebenen Tracking-Error gegenüber einer Benchmark und schließlich U² ein festes oder variables aber vorgegebenes quadratisches, mit den Kosten K bewertetes Maß für das Umschichtungsvolumen gegenüber einer Benchmark.
Optimierungsfunktionen: Ausgewertet am Beispiel des Minimum-Varianz-Portfolios.
Das Minimum-Varianz-Portfolio ist dadurch gekennzeichnet, dass es unter allen möglichen Portfoliozusammensetzungen dasjenige ist, welches die kleinste Varianz – also das kleinste Risiko – aufweist.
Die Lösung w* des Minimierungsproblems
L(w*) = min L(w)
wird berechnet, indem die Optimierungsfunktion
L = w’Cw + λ*(1 – w‘1)
einmal partiell nach dem Gewichtsvektor w und in einer zweiten Rechnung partiell nach dem Lagrange-Parameter λ abgeleitet wird. Beide Ableitungen werden zur Minimumbestimmung gleich Null gesetzt.
Ableitung der Optimierungsfunktion L nach w und gleich dem Nullvektor o setzten liefert:
(I) 2Cw + λ*1 = 0
Ableitung der Optimierungsfunktion L nach λ und gleich Null setzten liefert:
(II) 1 – w‘1 = 0
Anschließend wird die Gleichung (I) nach dem Gewichtsvektor w umgestellt, indem mit der inversen Kovarianzmatrix C–¹ multipliziert wird. Der Gewichtsvektor w berechnet sich dann zu
(III) w = (1/2)* λ*C–¹ 1
Dieses Ergebnis wird in die transponierte Gleichung (II)
(IIa) 1′w = 1
(IIb) (1/2)* λ*1′ C–¹ 1 = 1
eingesetzt. Weil 1′ C–¹ 1 eine Zahl ist, kann Gleichung (IIb) nach λ umgestellt werden. D. h. der vorher unbekannte Lagrange-Parameter λ lässt sich jetzt berechnen.
(IIc) λ = 2 / (1′ C–¹ 1)
Dieses Ergebnis wird nun in die Gleichung (III) eingesetzt und der Gewichtsvektor w berechnet sich abschließend zu
(IIIa) w = (C–¹ 1) / (1′ C–¹ 1)
Dieses ist das Endergebnis w* = w des Minimierungsproblems. Für diesen Gewichtsvektor nimmt die Optimierungsfunktion L(w) ihr Minimum an. Weil die Optimierungsfunktion L zu den quadratischen Optimierungsfunktionen zählt, ist die Kovarianzmatrix C gleich der Hessematrix. Darüber hinaus ist die Kovarianzmatrix C nach Konstruktion symmetrisch und positiv definit, sodass der ermittelte Extremwert von L tatsächlich ein Minimum darstellt.
Leicht ist jetzt die Gleichungsnebenbedingung in der Form (IIa) zu prüfen, indem w in der Gleichung (IIIa) von links mit 1′ multipliziert wird. Dann werden Zähler und Nenner in (IIIa) gleich und lassen sich kürzen, so dass schließlich das erwartete Ergebnis 1 übrig bleibt.
Nachdem die Frage der Zusammensetzung des Portfolios durch den Gewichtsvektor w beantwortet wird, bleibt abschließend noch zu klären, welches Risiko-Ertrag-Profil das Portfolio hat. Hierzu wird zunächst die Portfoliovarianz S² berechnet
S²
= w’Cw
= w’C (C–¹ 1) / (1′ C–¹ 1)
= (w’C C–¹ 1) / (1′ C–¹ 1)
= (w‚ 1) / (1′ C–¹ 1)
= 1 / (1′ C–¹ 1)
Die Portfoliorendite R berechnet sich abschließend zu
R
= r’w
= (r‚ C–¹ 1) / (1′ C–¹ 1)
Das Minimum-Varianzportfolio wird also durch den Gewichtsvektor w und das Risiko-Ertrag-Profil (S², R) charakterisiert.
![]()
![]()
![]()
Weil die Optimierungsfunktion L hier keine Ungleichungsnebenbedingungen für die Beschränkung der einzelnen Gewichte für die Vermögenswerte beinhaltet, können – je nach Datenlage die zur Kovarianzmatrix C führt – die Gewichte einzelner Vermögenswerte negativ sein. D.h. der Investor müsste in diesen Vermögenswerten eine Short-Position eingehen, um das Minimum-Varianz-Portfolio zusammenzusetzen.
Ungleichungsnebenbedingungen für Optimierungsfunktionen in der Portfoliotheorie
Die überwiegende Mehrheit aller Optimierungsproblem in der Portfoliotheorie, die sich in einer konkreten Ausgestaltung einer Optimierungsfunktion niederschlagen, verwendet als Ungleichungsnebenbedingung die Beschränkung der Gewichte w![]() einzelner oder aller Vermögenswerte. So können z. B. alle Vermögenswerte nach oben auf 100% und nach unten auf 0% beschränkt sein. Damit ist in diesem Beispiel gewährleistet, dass keine Short-Positionen in einzelnen Vermögenswerten nach Auswertung der Optimierungsfunktion auftreten. Ganz allegemein kann der Gewichtsvektor w in folgender Weise durch einen unteren und einen oberen Gewichtsvektor beschränkt sein:
einzelner oder aller Vermögenswerte. So können z. B. alle Vermögenswerte nach oben auf 100% und nach unten auf 0% beschränkt sein. Damit ist in diesem Beispiel gewährleistet, dass keine Short-Positionen in einzelnen Vermögenswerten nach Auswertung der Optimierungsfunktion auftreten. Ganz allegemein kann der Gewichtsvektor w in folgender Weise durch einen unteren und einen oberen Gewichtsvektor beschränkt sein:
w![]() w
w ![]() w
w![]() .
.
Für den unteren und den oberen Gewichtsvektor gelten für ein wohlbestimmtes Optimierungsproblem in der Portfoliotheorie folgende Bedingungen:
0 ![]() 1′w
1′w![]()
![]() 1′w
1′w![]() 1.
1.
Diese Bedingungen werden in der Regel als Bestandteil der Optimierungsfunktion betrachtet.
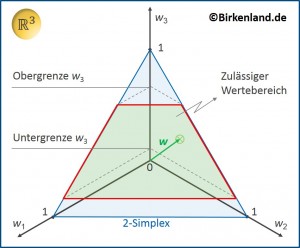 Die Abbildung zeigt die Darstellung eines Gewichtsvektors w in einem Koordinatensystem für ein Beispiel mit drei Vermögenswerten. In dem Beispiel ist der dritte Vermögenswert nach unten und nach oben beschränkt und die anderen beiden Vermögenswerte dürfen Gewichte zwischen 0 und 1 annehmen. Da zusätzlich die Summe aller Vermögenswerte 1 sein soll, kann der Gewichtsvektor nur Werte innerhalb des rot umrandeten Teils des 2-Simplex sein.
Die Abbildung zeigt die Darstellung eines Gewichtsvektors w in einem Koordinatensystem für ein Beispiel mit drei Vermögenswerten. In dem Beispiel ist der dritte Vermögenswert nach unten und nach oben beschränkt und die anderen beiden Vermögenswerte dürfen Gewichte zwischen 0 und 1 annehmen. Da zusätzlich die Summe aller Vermögenswerte 1 sein soll, kann der Gewichtsvektor nur Werte innerhalb des rot umrandeten Teils des 2-Simplex sein.
Allgemein ergibt sich bei n Vermögenswerten und der Beschränkung aller Vermögenswerte zwischen 0 und 1 als möglicher Werteraum für den Gewichtsvektor ein (n-1)-dimensionaler Simplex. Werden weitere Beschränkungen auferlegt, wie im oberen Beispiel, so sind die Lösungen der Optimierungsfunktion innerhalb eines Teils des (n-1)-dimensionalen Simplex zu finden.
Zusammenfassung: Die vollständige Optimierungsfunktion in der Portfoliotheorie
Eine vollständige Optimierungsfunktion in der Portfoliotheorie besteht aus
- Minimierungsfunktion
Das ist der Funktionsterm, der durch Variation des Gewichtsvektors w minimiert werden soll. - Gleichungsnebenbedingungen
Hierin enthalten sind alle Nebenbedingungen, die sich als Gleichung darstellen lassen. Die Gleichungsnebenbedingungen werden durch Lagrange-Parametern mit der Minimierungsfunktion verknüpft. - Ungleichungsnebenbedingungen
Hierin enthalten sind in der Portfoliotheorie im Allgemeinen (Wert-)Beschränkungen, die der Gewichtsvektor nach oben oder unten zu erfüllen hat.
Zur Lösung der vollumfänglichen Optimierungsfunktion in der Portfoliotheorie sind in den allermeisten Fällen numerische Optimierungsverfahren zu verwenden, um den optimalen Gewichtsvektor w* zu berechnen, der dann alle Nebenbedingungen erfüllt. Der theoretische Rahmen der noch weiter verallgemeinerten Optimierungsfunktionen und deren Lösungsmöglichkeiten wird durch die Karush-Kuhn-Tucker-Bedingungen gesteckt.