Kovarianzmatrix

Die Kovarianzmatrix $\bf C$ entstammt einem ganz allgemeinen mathematischen Rahmen und findet in vielen wissenschaftlichen Disziplinen ihre Anwendung. In der Portfoliotheorie kommt der Kovarianzmatrix bei der Vermögensstrukturierung in einem Portfolio eine besondere Rolle zu. Insbesondere im Zusammenhang mit Optimierungsfunktionen in der Portfoliotheorie ist die Kovarianzmatrix von herausragender Bedeutung.

Die Kovarianzmatrix in der Portfoliotheorie

Vorbereitend werden die Renditen $r_i$ von $n$ verschiedenen Vermögenswerte zu einem Vektor $\bf r \in \mathbb{R}^{n}$ zusammengefasst. In manchen Literaturen findet sich häufig auch die Bezeichnung Ertrag statt Rendite und es wird dann $\bf r$ als Ertragsvektor bezeichnet. Es wird nun angenommen, dass diese $n$ verschiedenen Vermögenswerte später zu dem finalen Portfolio gehören, dass im Rahmen der Portfoliotheorie abgeleitete werden soll. Die einzelnen Vermögenswerte sind allerdings im Allgemeinen nicht unabhängig voneinander. Ein Investor könnte beispielsweise folgende Systematik beobachten: steigen die Aktien, dann fallen tendenziell die Anleiherenditen, d.h. die Renditen der Vermögenswerte „Aktien“ und „Anleihen“ sind nicht unabhängig voneinander. Somit sind die Einträge $r_i$ des Renditevektors $\bf r$ nicht unabhängig voneinander.

Werden im Zeitverlauf über mehrere Wochen beispielsweise die Wochenschlusswerte der einzelnen Renditen $r_i$ notiert und jeweils zu einem Renditevektor ${\bf r}(k)$ für die $k$ -te Woche zusammengefasst, so ist im Allgemeinen zu beobachten, dass der ganze Renditevektor ein zufälliges Verhalten aufweist. Bei einem Würfel wird bei jedem Wurf eine einzelne Zahl zwischen 1 und 6 gewürfelt. Die Wahrscheinlichkeitsverteilung beim Würfel – genauer einem Laplace-Würfel – ist bekannt und entspricht der Gleichverteilung. Übertragen auf den Renditevektor bedeutet dies, jede Woche wird nicht eine einzelne Zahl „gewürfelt“, sondern ein ganzer Vektor mit $n$ Einträgen. Auch bei dem $n$ -dimensionalen Renditevektor wird in der Portfoliotheorie eine Wahrscheinlichkeitsverteilung unterstellt.

Mit der Wahrscheinlichkeitsverteilung bzw. mit der Wahrscheinlichkeitsdichte lassen sich dann berechnen:

Erwartungswert

${\bf \mu} = E[{\bf r}]$

mit ${\bf \mu} = (\mu_1, \mu_2, ...,\mu_n)$ ist der Vektor aller einzelnen Ertragserwartungen (Erwartungswert der Renditen) der Vermögenswerte bezeichnet. Die Erwartungswertbildung erfolgt in diesem Konzept mit der Wahrscheinlichkeitsverteilung, die den Realisierungen von $\bf r$ zugrunde liegt.

Kovarianz

${\bf C} = E[({\bf r} - {\bf \mu}) ({\bf r}' - {\bf \mu}')]$

In der eckigen Klammer der Erwartungswertbildung steht die Multiplikation eines $n$ -dimensionalen Spaltenvektors mit einem $n$ -dimensionalen Zeilenvektor. Das Ergebnis einer solchen Multiplikation ist eine $(n\times n)$ -dimensionale Zufallsmatrix, da der Vektor $\bf r$ der einzelnen Renditen ein Zufallsvektor ist. Wird über die einzelnen Einträge der Matrix abschließend der Erwartungswert gebildet, so berechnete sich die Kovarianzmatrix $\bf C$ .

Im Allgemeinen können mit Hilfe einer Verteilungsannahme die Werte für $\bf \mu$ und $\bf C$ aus den notierten Realisierungen ${\bf r}(k)$ geschätzt werden (Beispiel Likelihood-Methode). Sind die Werte bekannt, kann mit Hilfe der Kovarianzmatrix im Rahmen der Portfoliotheorie für ein Portfolio die Varianz berechnet werden.

Anwendungsbeispiel zur Kovarianzmatrix

Sei $R = {\bf r' w}$ die Portfoliorendite berechnet aus einer notierten Realisierung des $n$ -dimensionalen Renditevektors $\bf r$ . Der Portfolioertrag $R$ (die Rendite des Portfolios) ist dann eine Zufallszahl, die von der zufälligen Realisierung des Renditevektors abhängt. Ferner sei ${\= R} ={\bf \mu' w}$ der Erwartungswert des Portfolioertrags berechnet aus den Erwartungswerten $\mu_i$ der einzelnen Vermögenswerte des Portfolios. Die Varianz des Portfolios wird dann durch folgenden Erwartungswert gebildet:

$\begin{flalign*}\nonumber \text{Var}[R] & = E[(R-{\=R})^2] & \nonumber \\ & = E[(R-{\=R})'(R-{\=R})] & \nonumber \\ & = E[({\bf r' w}-{\bf \mu' w})'({\bf r' w}-{\bf \mu' w})] &\nonumber \\ & = E[({\bf w'r}-{\bf w' \mu})({\bf r' w}-{\bf \mu' w})] &\nonumber \\ & = E[{\bf w'}({\bf r}-{\bf \mu})({\bf r'}-{\bf \mu'}){\bf w}] &\nonumber \\ & = {\bf w'} E[({\bf r}-{\bf \mu})({\bf r'}-{\bf \mu'}) ] {\bf w} &\nonumber \\ & = {\bf w' C w} & \end{flalign*}$

In der Portfoliotheorie wird die Varianz des Portfolios oft mit $S^2$ bezeichnet. Einige Literaturquellen verwenden auch den zusammenfassenden Begriff Portfoliovarianz. Die Kovarianzmatrix ist in der Portfoliotheorie ein wichtiger Parameter, um für ein Portfolio das Risiko in einer Maßzahl – der Varianz – auszudrücken.

Eigenschaften der Kovarianzmatrix

Notiert werden Eigenschaften der Kovarianzmatrix $\bf C$ , die in der Portfoliotheorie von besonderer Bedeutung sind.

Auf der Hauptdiagonale der Kovaraianzmatrix stehen die Varianzen der einzelnen Vermögenswerte
Die Kovarianzmatrix ist in der Portfoliotheorie reell und symmetrisch.
Die Kovarianzmatrix ist positiv semidefinit, d. h. es gilt 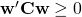${\bf w' C w} \ge 0$ und das für alle 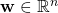${\bf w} \in \mathbb{R}^{n}$ . Diese Eigenschaft stellt sicher, dass die Portfoliovarianz 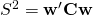$S^2 = {\bf w' C w}$ stets positiv ist.