Die Indikatoreins in der Portfoliotheorie
Viele Formeln und Berechnungen in der Portfoliotheorie lassen sich durch die Verwendung der sogenannten Indikatoreins deutlich vereinfachen. Das Konzept der Indikatoreins fußt auf der mathematischen Definition der Indikatorfunktion.
Die Indikatorfunktion
Die Indikatorfunktion stellt eine Abbildung f einer Menge M auf die Menge der Zahlen {0,1} dar. Die Indikatorfunktion mathematisch formal ausgedrückt lautet also:
f: M → {0,1}
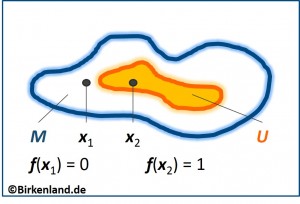
Die Indikatorfunktion besitzt folgende Eigenschaften. Sei U eine Teilmenge von M, es gilt also U ⊆ M, dann gilt für ein Element x von M, also für x∈M, dass der Wert der Indikatorfunktion 1 ist, wenn x in U liegt, wenn also gilt x∈U. Wenn x nicht in U liegt, wenn also gilt x∉U, dann ist der Wert der Indikatorfunktion 0. Formal gilt also:
f(x) = {1 wenn x∈U; 0 wenn x∉U}
Die nachfolgende Abbildung verdeutlicht die Indikatorfunktion noch einmal für zwei verschiedene Lagen von x.
Die Indikatoreins
Die Indikatoreins kann als eine diskrete Variante der Indikatorfunktion aufgefasst werden. Sind für einen Investor beispielsweise n verschiedene Vermögenswerte kaufbar, von denen er aber im Rahmen der Portfoliotheorie zur Vermögensstrukturierung lediglich m Vermögenswerte kaufen möchte, so kann er zur Darstellung des Sachverhalts die Indikatoreins nutzen.
Dabei geht er wie folgt vor:
- Er sortiert zunächst alle möglichen n Vermögenswerte gemäß eigener Kriterien in eine Reihenfolge, beispielsweise nach Ertrag oder Risiko sortiert.
- Diese Reihenfolge behält er in den weiteren Betrachtungen immer bei und verändert sie nicht.
- Dann werden die Vermögenswerte – wie in der Portfoliotheorie üblich – durchnummeriert:
i = 1, …, n. - Anschließend bildet er eine Liste in der n Mal die Zahl 1 steht:
1′ = (1, 1, 1, …,1).
In der Fachsprache ausgedrückt: Der Investor erhält einen n-dimensionalen Zeilenvektor, der lauter 1-er enthält. Dieser Vektor ist die vollbesetzte Indikatoreins und wird auch Einsvektor genannt. - Will er die Anwendung der Portfoliotheorie auf seine Bedürfnisse anpassen, so verändert er die Indikatoreins 1′ wie folgt: Er schreibt an jede Position in dem Vektor eine Null, wenn er den entsprechenden Vermögenswert in den weiteren Portfolioüberlegungen nicht betrachten möchte.
- Abschließend erhält er also die Indikatoreins, die nun lediglich m Mal die Zahl 1 zeigt. Diese Indikatoreins bildet seine Vorgaben bezüglich der von ihm als kaufbar eingestuften Vermögenswerte ab.
Beispiel für eine Indikatoreins:
Α = (1, 0, 1, 0, 1, 1, 1, 0, 0, 1)
Es gibt also 10 mögliche Vermögenswerte, die in einer Portfoliotheorie genutzt werden könnten, von denen der Investor aber lediglich 6 kaufen möchte. Zur Unterscheidung wird die investorenspezifische Indikatoreins mit Α bezeichnet und die vollbesetzte Indikatoreins mit 1′.
Bildlicht gesprochen, die Indikatoreins Α projiziert aus der Menge M, die alle möglichen Vermögenswerte enthält, diejenigen heraus, die zu der vom Investor als kaufbare benannten Untermenge U gehören.
Portfoliotheorie mit der Indikatoreins
Um die Formeln der Portfoliotheorie weiter zu vereinfachen, wird in der Regel – es gibt besondere Abweichungen, beispielsweise im Zusammenhang mit dem portfoliotheoretischen Konzept des Tracking-Errors – nicht die investorenspezifische Indikatoreins Α sondern die von vornherein auf den Unterraum U beschränkte Indikatoreins verwendet. D.h. die nicht kaufbaren Vermögenswerte werden von Anfang an aus der Liste herausgelassen und nur noch die tatsächlich kaufbaren Vermögenswerte betrachtet. Insofern wird direkt mit einer auf m Dimensionen beschränkten vollbesetzten Indikatoreins, also mit dem Einsvektor entsprechender Dimension, gerechnet. Ohne weitere Unterscheidung kann dann mit dem Symbol 1′ in der Portfoliotheorie weitergerechnet werden und es wird außerdem n = m gesetzt.
Als Anwendungsbeispiel wird im Folgenden die für die Portfoliotheorie wichtige Nebenbedingung betrachtet, dass die Summe aller Vermögenswerte in den Portfolien gleich 1 sein soll. D.h. übersetzt, es können nur 100% des Kapitals angelegt werden.
In der Portfoliotheorie wird dazu für jeden Vermögenswert i ein Portfoliogewicht wi berechnet, wobei gilt i = 1, …, n. Das Portfoliogewicht wi errechnet sich als investiertes Kapital im Vermögenswert i geteilt durch das gesamte investierte Kapital. Werden alle einzelnen Portfoliogewichte in einer Liste zusammengefasst, so zeigt sich ein neuer Vektor, der in der Portfoliotheorie als Gewichtsvektor w = (w1, w2, …, wn) bekannt ist.
Die Nebenbedingung besagt nun, dass Folgendes gelten muss:
1 = w1 + w2 + … + wn.
Manchmal findet sich in der Portfoliotheorie auch die abkürzende Darstellung 1 = ∑wi.
In der Mathematik gibt es die Konstruktion des Skalarproduktes zweier Vektoren. Wenn zwei Vektoren a und b skalar miteinander mulitpliziert werden a’b (Zeilen- mal Spaltenvektor), so ist das Ergebnis eine Zahl c = a1*b1 + a2*b2 + … + an*bn. Dieser Zusammenhang wird in der Portfoliotheorie ausgenutzt und obige Gleichung wird umgeschrieben zu
1 = 1*w1 + 1*w2 + … + 1*wn.
Rückwärts betrachtet, ist dieses das Skalarprodukt der Indikatoreins 1′ mit dem Gewichtsvektor w. D.h. die Nebenbedingung wird mit der Indikatoreins zu
1 = 1′w