Portfoliomanagement: Extremwertstatistik zur Risikobewertung bei 5 Mrd. Euro Stiftungsvermögen.
Bei der Verwaltung eines Vermögens unterliegt der Portfoliomanager bestimmten Rahmenbedingungen, die in der Praxis in den Anlagerichtlinien aufgelistet sind.
Die Anlagerichtlinien können vom Vermögensinhaber frei vorgegeben werden oder ergeben sich aus rechtlichen Vorgaben, sowie Satzungen oder Geschäftsordnungen der betreffenden Institution.
Diese vorgegebenen Anlagerichtlinien entfalten ihre Wirkung unter anderem dadurch, dass der Anteil einzelner Vermögenswerte beschränkt ist. Beispiel: Der Anteil der Aktien am Gesamtvermögenswert darf maximal 5 % betragen.
Neben Anteilsbeschränkungen können Anlagerichtlinien aber auch Vorgaben hinsichtlich des mit dem Engagement verbundenen Risikos enthalten.
Die Risikobewertung und die Maßnahmen zur Risikobegrenzung sind in der Regel auch in den Anlagerichtlinien festgelegt.
Insbesondere für konservative Portfolios, bei denen das Kapital gemäß Anlagerichtlinie zum überwiegenden Teil in sehr sicheren Vermögenswerten investiert ist, werden dem Portfoliomanager oft strenge Vorgaben zur Risikobegrenzung auferlegt.
Zu den Risikobegrenzungen zählen z. B. Vorgaben zur Schwankungsbreite des Anlagevolumens innerhalb eines Kalenderjahres (Volatilität) oder die innerhalb einer Haltedauer mit einer gegebenen Wahrscheinlichkeit nicht zu überschreitende Verlusthöhe (Value-at-Risk).
Ein anderer in der Anlagerichtlinie geregelter Sachverhalt steht im Zusammenhang mit der Risikobewertung und befasst sich u. a. mit Vermögensminima.
Es kann per Anlagerichtlinie dem Portfoliomanager beispielsweise die Pflicht zur Abschätzung des möglichen minimalen Vermögens in der kommenden Berichtsperiode – häufig dem nächsten Kalenderjahr – auferlegt werden.
Im Kern geht es dabei um eine Risikobewertung und eine Prognose darüber, welcher maximale Verlust im extremen Fall zu erwarten ist, so dass das Vermögen dann einen minimalen Wert annimmt.
Derartige nach vorne gerichteten Risikobewertungen sind im Rahmen der Extremwertstatistik ableitbar und sind im Allgemeinen Bestandteil des jährlichen Risikoreports des Portfoliomanagers.
Die Extremwertstatistik in der Naturwissenschaft beschäftigt sich hauptsächlich damit, Methoden zur Verfügung zu stellen, die zur mathematischen Beschreibung von extrem großen (Hochwasser) bzw. extrem kleinen (Kälterekorde) und damit in beiden Fällen sehr seltene Ereignissen geeignet sind.
Diese Methoden können ohne wesentlichen Aufwand zur Risikobewertung im Portfoliomanagement genutzt werden.
Wie die Risikobewertung im Portfoliomanagement mit Hilfe der Extremwertstatistik genau durchgeführt werden kann, soll im Folgenden allgemein und anhand eines Stiftungsvermögens als durchgängig genutztes, idealisiertes Beispiel erläutert werden.
Beispiel: Stiftungsvermögen
Als Institution betrachten wir eine Stiftung mit einem Stiftungsvermögen von 5 Mrd. Euro. Zustiftungen, Abflüsse und Zinszahlungen, sowie die Bewegungen an den Kapitalmärkten beeinflussen das Stiftungsvermögen.
Zur Vereinfachung wird angenommen, dass jeweils zum Wochenstart das Stiftungsvermögen 5 Mrd. Euro beträgt und die beeinflussenden Faktoren im Verlauf der Woche zu einer Vermögensveränderung führen.
Zum Wochenschluss wird der veränderte Vermögensstand notiert und bis zum Start der neuen Woche wird das Vermögen wieder auf 5 Mrd. Euro zurückgeführt.
Dieses vereinfachte, idealisierte Beispiel soll im Folgenden dazu dienen, um die Grundidee und die Anwendung der Extremwertstatistik zu verdeutlichen.
Viele Modifikationen des Beispiels sind denkbar und ebenfalls im Rahmen der Extremwertstatistik bewertbar.
Zu den Modifikationen zählen beispielsweise:
- Berücksichtigung von Trends
- Wachstumsprozesse
- Einhaltung von Wertsicherungsgrenzen
- Statistische Modellierung der Zu- und Abflüsse
Um die Grundidee der Anwendung der Extremwertstatistik im Portfoliomanagement zu zeigen, reicht aber das vereinfachte Beispiel aus, auf das wir uns hier fokussieren.
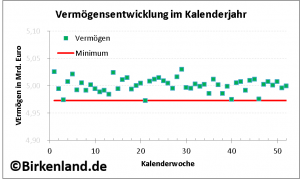
Die nachfolgende Grafik zeigt die Vermögensstände der als Beispiel angenommenen Stiftung jeweils zum Wochenschluss im letzten Kalenderjahr.
Als erste Auswertung ist das absolute Minimum des Vermögens im letzten Kalenderjahr als untere Begrenzungslinie (rot) eingezeichnet.
Stützt sich der Portfoliomanager auf eine einfache Prognose, so geht er davon aus, dass dieser Wert auch im kommenden Berichtszeitraum angenommen werden kann.
D. h. mit der Annahme „so wie es letztes Jahr war, wird es im nächsten Jahr auch“ läge eine Prognose des minimalen Vermögens und somit eine nach vorne gerichtete Risikobewertung vor.
Die folgenden Überlegungen führen dazu, von diesem (naiven) Prognoseverfahren zu einem fundierten, aus der Extremwertstatistik abgeleiteten Verfahren zu gelangen.
Exkurs: Naturforschung und Extremwertstatistik
Lange bekannt und angewendet sind in der Naturforschung die Methoden der Extremwertstatistik. Diese Methoden erlauben Aussagen und Prognosen über extreme Naturereignisse.
Zu den dort untersuchten extremen Ereignissen zählen z. B. die maximale Höhe von Sturmfluten, die maximalen Windgeschwindigkeiten in einer Region, die maximale Magnitude bei einem Erdbeben oder die maximale Temperatur in einer Region.
Die Untersuchungen zielen in diesen Forschungsgebieten darauf ab, künftige Entwicklungen des betrachteten Naturphänomens abzuschätzen.
Diese Abschätzung umfasst idealerweise die Angabe eines zu erwartenden Maximalwertes innerhalb eines bestimmten Zeithorizonts, sowie die Eingrenzung des erwarteten Maximalwertes in ein bestimmtes Werteintervall.
Beispiel für eine Prognose im Rahmen der Extremwertstatistik: Im kommenden Jahr wird an einem Hafenabschnitt eine Sturmflut mit einer maximalen Höhe im Wertebereich von 7,80 Meter bis 8,20 Meter erwartet. Der Erwartungswert der maximalen Sturmflut wird mit 8,00 Metern angegeben.
Daneben werden bei Naturereignissen mit der Extremwertstatistik noch Jährlichkeiten berechnet, die Aussagen über Wiederkehrintervalle von Extremereignissen machen.
Diese Bewertungen führen in der Regel zu technischen Vorkehrungen, um sich vor den Zerstörungen der möglicherweise eintretenden Extremereignisse zu schützen: Höhe eines Deichs, Windabweiser an Gebäuden, Erdbebenabsicherung von Gebäuden, Dicke von Isolierschichten, etc.
Extremwertstatistik im Portfoliomanagement
Die Extremwertstatistik erlaubt aber nicht nur Aussagen über Maximalwerte, sondern ist ebenso anwendbar für Fragestellungen im Zusammenhang von Minimalwerten. Die Extremwertstatistik liefert auch hierbei den Wert des zu erwartenden Minima und dessen Eingrenzung in ein Werteintervall.
Während in der Naturforschung die Analyse der Minima keine ausgeprägte Rolle spielt, ist aber die Untersuchung der Minima für das Portfoliomanagement interessant.
Bei der Verwaltung von Vermögenswerten kann z. B. bei einem bestehenden Portfolio aufgrund der Anlagerichtlinien folgende Frage aufkommen: In welcher Größenordnung liegt das zu erwartende minimale Vermögen, wenn ein maximaler Verlust eintritt?
Derartige Fragen erlangen im Portfoliomanagement – spätestens seit den Anschlägen vom 11.09.2001 und der Finanzkrise im Jahr 2008 – zunehmend an Bedeutung.
Da beim Eintreten des maximalen Verlusts ein minimales Vermögen zu verzeichnen ist, kann die Anwendung der Extremwertstatistik wahlweise auf den maximalen Verlust oder das minimale Vermögen ausgerichtet sein.
Anwendungsfälle der Extremwertstatistik im Portfoliomanagement
Die Extremwertstatistik kann bei einem verwalteten Portfolio dann wichtig werden, wenn es z. B. aufgrund der Anlagerichtlinien konkrete Vorgaben hinsichtlich eines minimal vorzuhaltenden Vermögens gibt.
Beispiele für Vorgaben im Rahmen der Anlagerichtlinien, die zur Anwendung der Extremwertstatistik führen können:
- Ein minimal (rechtlich) gefordertes Sicherungskapital als Hinterlegung bei anderweitigem Risikoengagement der betreffenden Institution.
- Eine kundenseitig geforderte Mindesthöhe des Portfoliowerts im Rahmen einer Finanzportfolioverwaltung.
- Per Satzung zweckgebundene Stiftungsgelder, die ein bestimmtes Mindestvolumen nicht unterschreiten dürfen.
Beispiele für Portfolios, die mit den Methoden der Extremwertstatistik analysiert werden können:
- Eigenkapitalhinterlegungen bei Banken
- Deckungskapital in der Versicherungswirtschaft
- Stiftungsvermögen
Auch wenn die Anlagerichtlinie es nicht explizit vorgibt, kann insbesondere aber im Rahmen eines Stresstests die Frage nach einem minimalen Vermögensbestand aufkommen und dessen statistischer Bewertung mit Methoden der Extremwertstatistik angezeigt sein.
Verwendung der Ergebnisse der Extremwertstatistik
Die Ergebnisse der Extremwertstatistik können für den Vergleich mit einem vorgegebenem Schwellwert (beispielsweise einem Verlustlimit) genutzt werden.
Ist das Ergebnis der Analyse nicht mit dem Schwellwert vereinbar (beispielsweise liegt der erwartete maximale Verlust über dem Schwellwert), so folgt in der Regel eine Neuberechnung der Portfoliozusammensetzung.
Die neue Soll-Zusammensetzung wird vor dem Hintergrund sämtlicher Nebenbedingungen im Rahmen einer Portfoliooptimierung bestimmt.
Ein Vergleich der Ist- mit der Soll-Zusammensetzung des Portfolios liefert sodann eine Handlungsstrategie zur Umschichtung von Vermögenswerten im bestehenden Portfolio, so dass die rechtlichen, aufsichtsrechtlichen und/oder satzungsmäßigen Vorgaben erfüllt werden können.
Abgrenzung der Extremwertstatistik von anderen Verfahren
Die hier betrachtete Extremwertstatistik und die daraus abgeleiteten Aussagen sind zu unterscheiden von statistischen Analysen zu Risikomaßen, die auf Downside-Risiken abstellen.
Die Downside-Risikomaße erfassen – vereinfacht ausgedrückt – lediglich negative Abweichungen von einer vorgegebenen Schranke, beispielsweise einer vorgegebenen unteren Zielrendite eines Portfolios.
Als wichtiges Merkmal wird in der Extremwertstatistik keine Schranke – ab der ein Schaden eintritt – vorgegeben, sondern die Anwendung der Methoden der Extremwertstatistik liefert im Idealfall ein Wertintervall in dem sich eine mögliche untere Begrenzung mit einer bestimmten Wahrscheinlichkeit befindet.
Diese Begrenzung kann anschließend mit einem vorgegebenen Schwellwert verglichen werden.
Obwohl eine gewisse Ähnlichkeit der Extremwertstatistik zu den sogenannten Drawdowns einer Finanzinvestition besteht, sind aber im Rahmen der Extremwertstatistik weitere, das minimale Vermögen betreffende Aussagen möglich.
Während der Drawdown – heuristisch betrachtet – den in der Vergangenheit maximal eingetretenen Verlust als einzelne Zahl ausweist und nur bedingt Prognosen über künftige Drawdowns bei der Finanzinvestition erlaubt, liefert die Extremwertstatistik weitere Kenngrößen, die als Risikobewertung und Prognose dienen können.
Die Anwendung der Extremwertstatistik im Rahmen des Portfoliomanagements liefert als Basis für weitere Berechnungen die Wahrscheinlichkeitsverteilung des minimalen Vermögenswertes.
Mit der Wahrscheinlichkeitsverteilung lassen sich sämtliche statistischen Kenngrößen berechnen. Dazu zählen insbesondere der Erwartungswert und die Streuung des minimalen Vermögenswertes.
Die Streuung definiert einen Wertebereich um den Erwartungswert des minimalen Vermögenswertes. Dieser Wertebereich kann als Risikobewertung im Risikoreport ausgewiesen werden.
Mit der Wahrscheinlichkeitsverteilung kann zusätzlich ausgerechnet werden, wie wahrscheinlich ein erneuter minimaler Vermögenswert innerhalb des vorgenannten oder eines beliebig vorgegebenen Wertebereichs ist.
Diese Vorgehensweise liefert also beispielsweise eine Antwort auf die Frage: Wenn im nächsten Jahr ein minimales Vermögen auftritt, wie wahrscheinlich ist es, dass dieses in einem bestimmten Wertebereich liegt?
Bemerkung: Manchmal wird der Erwartungswert des minimalen Vermögens auch als extreme Value-at-Risk (eVaR) bezeichnet.
Extremwertstatistik im Portfoliomanagement: Übersicht der Vorgehensweise
Die nachfolgende Grafik zeigt die wesentlichen Schritte von der Datenerhebung bis zum Risikoreport auf, die ein Portfoliomanager zur adäquaten Risikobewertung im Rahmen der Extremwertstatistik bearbeiten sollte.
 Diese Vorgehensweise soll im Folgenden weiter verdeutlicht werden. Für das Beispiel des Stiftungsvermögens ist der erste Schritt – Datenerhebung – in der obigen Abbildung 1 bereits erfolgt.
Diese Vorgehensweise soll im Folgenden weiter verdeutlicht werden. Für das Beispiel des Stiftungsvermögens ist der erste Schritt – Datenerhebung – in der obigen Abbildung 1 bereits erfolgt.
Extremwertstatistik im Portfoliomanagement: Theorie
Die statistischen Ereignisse eines betrachteten Vorgangs, werden im Allgemeinen mit der kumulierten Wahrscheinlichkeitsverteilungsfunktion (im Folgenden kurz: Verteilung) ![]() bzw. mit der Wahrscheinlichkeitsdichtefunktion (im Folgenden kurz: Dichte)
bzw. mit der Wahrscheinlichkeitsdichtefunktion (im Folgenden kurz: Dichte) ![]() beschrieben.
beschrieben.
Als Variablen werden Zufallsgrößen ![]() betrachtet, die unter Zufallsbedingungen Werte
betrachtet, die unter Zufallsbedingungen Werte ![]() aus einem reellen Bereich als Teilmenge von
aus einem reellen Bereich als Teilmenge von ![]() annehmen können. Die zufälligen Ereignisse
annehmen können. Die zufälligen Ereignisse ![]() sind dann Realisierungen der Zufallsgröße
sind dann Realisierungen der Zufallsgröße ![]() .
.
Verteilung und Dichte hängen über folgenden mathematischen Ausdruck zusammen:
![]()
Hinweis: Da keine Verwechslung mit der oberen Integralgrenze möglich ist, wird hier die Integrationsveränderliche ebenfalls mit ![]() bezeichnet.
bezeichnet.
Die kumulative Verteilungsfunktion ![]() entspricht der Wahrscheinlichkeit
entspricht der Wahrscheinlichkeit ![]() , dass die Zufallsgröße
, dass die Zufallsgröße ![]() eines Zufallsprozesses Werte kleiner als
eines Zufallsprozesses Werte kleiner als ![]() annimmt:
annimmt:
![]()
Ist die Verteilung ![]() bekannt, so kann durch Differentiation nach der oberen Integralgrenze die Dichte bestimmt werden:
bekannt, so kann durch Differentiation nach der oberen Integralgrenze die Dichte bestimmt werden:
![]()
Dichte- und Verteilungsfunktion
Viele Anwendungsfälle in der Praxis betrachten die Verteilung von Maximalwerten, die in einer Beobachtungsperiode auftreten. Der Maximalwert eines Hochwassers innerhalb eines Jahres ist hier ein anschauliches Beispiel.
Zur Beschreibung der Statistik von Maximalwerten liegen unterschiedliche Dichten und Verteilungen vor:
- Allgemeine Extremwertverteilung
- Exponentialverteilung
- Fréchet-Verteilung
- Gammaverteilung
- Gumbel-Verteilung
- Logarithmische Normalverteilung
- Pearson III-Verteilung und logarithmische Pearson III-Verteilung
- Weibull-Verteilung und logarithmische Weibull-Verteilung
Vergleiche hierzu und für weitere Beispiele aus der Hydrologie folgende Quellen: Einführung Extremwertstatistik oder Bestimmung hydrologischer Bemessungsgrundlagen.
Welche Dichte oder Verteilung zur Beschreibung des jeweiligen Sachverhalts geeignet ist, kann im Vorhinein oft nur schwer abgeschätzt werden. In der Hydrologie werden daher meist verschiedene Dichten oder Verteilungen genutzt und anschließend durch Auswertung weiterer Gütekriterien eine Wahl getroffen.
Im Allgemeinen werden vordefinierte Gütekriterien im Rahmen von qualitativen und quantitativen Anpassungstests ausgewertet.
In die qualitativen Anpassungstests fließen dabei meist noch weitere hydrologische Überlegungen, regionale Besonderheiten und das Extrapolationsverhalten im Zusammenhang mit der hydrologisch eingeschätzten Jährlichkeit des Höchstwertes ein.
Die qualitativen Anpassungstests münden häufig in einem optischen Vergleich der empirischen – also aus den Messwerten gewonnenen – und der theoretischen Dichte bzw. Verteilung.
Quantitative Anpassungstests sind in der Regel als Hypothesentests ausgelegt.
Auswahl an Beispielen für Hypothesentests:
- Chi-Quadrat-Test
- Cramér-von-Mises-Test
- Anderson-Darling-Test
- Kullback-Leibler-Divergenz
- Akaike-Informationskriterium
- Kolmogorow-Smirnow-Test
In der Hydrologie können Analysen häufig anhand von Messreihen durchgeführt werden, die fünfzig und mehr Jahre umfassen.
Damit können die vorgenannten quantitativen Methoden die Güte einer bestimmten angepassten Dichte und Verteilung herausstellen. Die Güte ermöglicht darüber hinaus eine abschließende Entscheidung für oder gegen die Verwendung der angepassten Dichte einer Verteilung.
Derartige viele Beobachtungsdaten liegen bei einem verwalteten Vermögen im Portfoliomanagement in der Regel nicht vor, so dass nur wenige Anpassungstests eine geeignete Gütebewertung erlauben.
Bei sehr kleinem Datenumfang bieten sich – wie wir weiter unten sehen werden – die optischen Vergleiche im Rahmen von speziellen Grafiken als qualitative Überprüfung an.
Für die quantitative Gütebestimmung bei wenigen Daten ist der einfach handhabbare Kolmogorow-Smirnow-Test nutzbar, der direkt die Verteilungsfunktion bewertet und gegenüber dem häufig eingesetzten Chi-Quadrat-Test den Vorteil hat, dass er ohne Klasseneinteilung angewendet werden kann.
Auswahl der Dichte- und Verteilungsfunktion
In den meisten praktischen Anwendungsfällen wird in einer ersten Auswahl von Verteilungsfunktionen die allgemeine Extremwertverteilung berücksichtigt und an die vorhandenen Messdaten angepasst.
Sie hat den Vorteil, dass sie die Gumbel-, Fréchet- und Weibull-Verteilung als Spezialfälle enthält. Es sind somit keine gesonderten Anpassungen an die Messdaten erforderlich, um diese drei Verteilungen auf Nutzbarkeit zu überprüfen.
Die allgemeine Extremwertverteilung soll daher im Folgenden als Ausgangspunkt dienen.
Eine vorgelagerte Koordinatentransformation ermöglicht die Beschreibung von Minima mit Hilfe der allgemeinen Extremwertverteilung.
Es wird sich zeigen, dass im Beispiel des Stiftungsvermögens die allgemeine Extremwertverteilung für Minima in die Gumbel-Verteilung für Minima übergeht.
Diese Gumbel-Verteilung wird für das Beispiel der Stiftung angepasst und einem Kolmogorow-Smirnow-Test unterzogen, um die Güte der Anpassung zu bewerten.
Wir nutzen abschließend die Gumbel-Verteilung der Minima des Stiftungsvermögens, um aufzuzeigen, wie eine verbesserte Risikobewertung im Zusammenhang mit der Prognose eines minimalen Vermögens im Portfoliomanagement vorgenommen werden kann.
Allgemeine Extremwertverteilung für Maximalwerte
Bei der Dichte der allgemeinen Extremwertverteilung handelt es sich um eine drei-parametrige Funktion der Form:
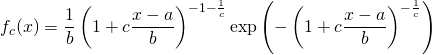
In der Dichte ![]() beschreibt
beschreibt ![]() den Lageparameter der Dichte und entspricht anschaulich, dem Hochpunkt der Dichte.
den Lageparameter der Dichte und entspricht anschaulich, dem Hochpunkt der Dichte.
Verändert sich ![]() , so verschiebt sich die Dichte entlang der
, so verschiebt sich die Dichte entlang der ![]() -Achse.
-Achse.
Der Parameter ![]() ist ein Streuungsparameter und bestimmt – etwas bildhaft beschrieben – die Breite der Dichte über der
ist ein Streuungsparameter und bestimmt – etwas bildhaft beschrieben – die Breite der Dichte über der ![]() -Achse.
-Achse.
Mit ansteigendem ![]() wird die Dichte flacher und breiter.
wird die Dichte flacher und breiter.
Damit erstrecken sich die möglichen Maxima – z. B. des Hochwassers in der Hydrologie – bei größerem ![]() über einen größeren Bereich.
über einen größeren Bereich.
Mit dem Parameter ![]() wird schließlich die Form der Dichte beeinflusst.
wird schließlich die Form der Dichte beeinflusst.
Es werden drei Grundformen als Spezialfälle der Dichte unterschieden:
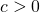 entspricht dem Typ Fréchet-Verteilung
entspricht dem Typ Fréchet-Verteilung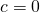 entspricht dem Typ Gumbel-Verteilung
entspricht dem Typ Gumbel-Verteilung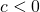 entspricht dem Typ Weibull-Verteilung
entspricht dem Typ Weibull-Verteilung
Anpassung der Verteilungsparameter
Die Verteilungsparameter ![]() und
und ![]() können durch Anpassung an die empirisch ermittelten Messwerte – bspw. die maximalen Hochwasser der letzten Jahre – bestimmt werden.
können durch Anpassung an die empirisch ermittelten Messwerte – bspw. die maximalen Hochwasser der letzten Jahre – bestimmt werden.
Es gibt mehrere Möglichkeiten die Anpassung der Parameter durchzuführen.
Zwei der bekanntesten Möglichkeiten sind die Anpassung der Parameter mit Hilfe der Maximum-Likelihood-Methode und der Momentenmethode.
Im Allgemeinen führen beide Verfahren auf leicht unterschiedliche Parameter und es ist im Nachhinein zu prüfen, welcher Parametersatz der Verteilung geeigneter ist, um die vorliegenden Messwerte zu beschreiben.
Hinweis: Zur Anwendung der Maximum-Likelihood-Methode ist in der Regel eine spezielle kaufbare (MatLab, Mathematica, etc.) oder selbst programmierte Software nötig, um die Parameter ![]() und
und ![]() an die Messwerte anzupassen.
an die Messwerte anzupassen.
Koordinatentransformation
Die vorgenannte Dichte ![]() und die zugehörige Verteilung
und die zugehörige Verteilung ![]() beschreiben Ereignisse, die mit Maximalwerten in Verbindung stehen, d. h. die Werte
beschreiben Ereignisse, die mit Maximalwerten in Verbindung stehen, d. h. die Werte ![]() stehen für mögliche Maximalwerte.
stehen für mögliche Maximalwerte.
Für die Anwendung der Extremwertstatistik im Portfoliomanagement werden Dichte und Verteilung für Minimalwerte eines Zufallsprozesses benötigt, um z. B. das Risiko eines auftretenden minimalen Vermögens in einer Beobachtungsperiode bewerten zu können.
Die gesuchte Dichte ![]() und die zugehörige Verteilung
und die zugehörige Verteilung ![]() für die Minima eines Zufallsprozesses können aus der Dichte
für die Minima eines Zufallsprozesses können aus der Dichte ![]() und Verteilung
und Verteilung ![]() der allgemeinen Extremwertverteilung für die Maxima durch eine Koordinatentransformation hergeleitet werden.
der allgemeinen Extremwertverteilung für die Maxima durch eine Koordinatentransformation hergeleitet werden.
Wir führen eine Hilfsvariable ![]() ein und definieren folgende Koordinatentransformation:
ein und definieren folgende Koordinatentransformation:
![]()
Anschaulich wird durch diese Koordinatentransformation die Dichte ![]() gespiegelt und an den Punkt
gespiegelt und an den Punkt ![]() verschoben.
verschoben.
Wir zeigen die Koordinatentransformation im Einzelnen.
Ausgangspunkt bildet der Zusammenhang zwischen Dichte und Verteilung:
![]()
In dieser Gleichung ist nun die Koordinatentransformation ![]() anzuwenden.
anzuwenden.
Aus der Transformation berechnen sich folgende Ersetzungen:
![]()
Wir berechnen nun die Obergrenze des transformierten Integrals:
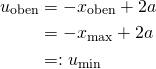
Damit folgt für das Argument in ![]() :
:
![]()
Die neue Untergrenze berechnet sich gemäß:
![]()
Diese Ersetzungen führen auf folgende Veränderungen des Integrals:
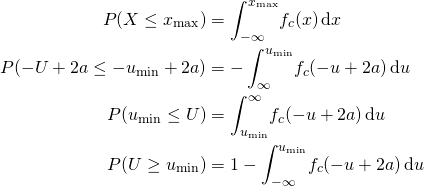
Das Integral in der letzten Zeile entspricht der Wahrscheinlichkeit, dass die Zufallsgröße ![]() Werte kleiner als
Werte kleiner als ![]() annimmt.
annimmt.
D. h. es gilt:
![]()
Bemerkung: ![]() .
.
Ersetzen wir ![]() durch ein allgemeines
durch ein allgemeines ![]() folgt schließlich die gesuchte Verteilung
folgt schließlich die gesuchte Verteilung ![]() für die Minima:
für die Minima:
![]()
Die Ableitung der Verteilung ![]() nach der oberen Integralgrenze führt auf die Dichte der Verteilung für die Minima:
nach der oberen Integralgrenze führt auf die Dichte der Verteilung für die Minima:
![]()
Allgemeine Extremwertverteilung für Minimalwerte
Die vorhergehende Gleichung besagt, dass an jeder Stelle ![]() in
in ![]() der Ausdruck
der Ausdruck ![]() eingesetzt wird, um
eingesetzt wird, um ![]() zu erhalten.
zu erhalten.
Da nach der Transformation von ![]() ausschließlich die Minimalwerte und nicht die Maximalwerte weiter analysiert werden, benennen wir nach der Transformation noch die Variable
ausschließlich die Minimalwerte und nicht die Maximalwerte weiter analysiert werden, benennen wir nach der Transformation noch die Variable ![]() in
in ![]() um.
um.
Als Ergebnis liegt somit nun die Dichte ![]() für die Minimalwerte eines Zufallsprozesses vor:
für die Minimalwerte eines Zufallsprozesses vor:
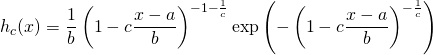
Ein direkter Vergleich von ![]() und
und ![]() zeigt, dass durch die Koordinatentransformation lediglich das Vorzeichen vor dem Formparameter
zeigt, dass durch die Koordinatentransformation lediglich das Vorzeichen vor dem Formparameter ![]() in der Klammer wechselt. Bei den Exponenten ändert sich dagegen das Vorzeichen vor dem Parameter
in der Klammer wechselt. Bei den Exponenten ändert sich dagegen das Vorzeichen vor dem Parameter ![]() nicht.
nicht.
In der Dichte ![]() repräsentiert die unabhängige Variable
repräsentiert die unabhängige Variable ![]() nun die Minimalwerte eines Zufallsprozesses.
nun die Minimalwerte eines Zufallsprozesses.
Extremwertstatistik im Portfoliomanagement: Anwendung
Liegen historische Daten eines bestehenden Portfolios vor, z. B. die Wochenschlusswerte der vergangenen Dekade, so kann eine Analyse der Daten erfolgen.
Als Anwendungsbeispiel betrachten wir wieder das Stiftungsvermögen.
Insgesamt erstreckt sich für dieses Beispiel das zur Verfügung stehende Datenmaterial über die letzten zehn Kalenderjahre.
Die obige Abbildung 1 zeigte hieraus beispielhaft die 52 Wochenschlusswerte des Stiftungsvermögens im letzten Kalenderjahr.
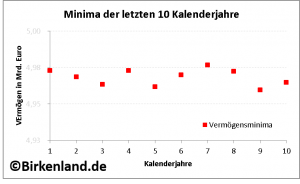
In jedem Kalenderjahr der vergangenen zehn Jahren wird nun das Minimum der ermittelten Wochenschlusswerte bestimmt.
Die folgende Grafik zeigt diese zehn Vermögensminima für das Stiftungsvermögen.
Im Ergebnis liegt nun eine Liste von zehn Minima von Wochenwertveränderungen vor, die jeweils innerhalb einer Jahresperiode in der Vergangenheit aufgetreten sind.
Anpassung der Dichte der allgemeinen Extremwertverteilung für die Minima
Für das Beispiel des Stiftungsvermögens ergab eine Anpassung der Dichte ![]() mit Hilfe der Maximum-Likelihood-Methode, dass der Parameter
mit Hilfe der Maximum-Likelihood-Methode, dass der Parameter ![]() sehr nahe bei null liegt.
sehr nahe bei null liegt.
Der Grenzübergang ![]() führt zu dem Spezialfall der allgemeinen Extremwertverteilung, der der Gumbel-Verteilung entspricht.
führt zu dem Spezialfall der allgemeinen Extremwertverteilung, der der Gumbel-Verteilung entspricht.
Es handelt sich dabei um eine zwei-parametrige Dichte ![]() mit der Darstellung:
mit der Darstellung:
![]()
Diese Dichte ist das negative Pendant zur Dichte der Gumbel-Verteilung für Maximalwerte und ist auch ein Spezialfall aus der Klasse der parametrisierten Dichten der Gompertz-Verteilungen, vgl. Anhang (a).
Wird die Dichte ![]() der Gumbel-Verteilung für Minimalwerte integriert so erhalten wir den mathematischen Ausdruck für die Gumbel-Verteilung
der Gumbel-Verteilung für Minimalwerte integriert so erhalten wir den mathematischen Ausdruck für die Gumbel-Verteilung ![]() :
:
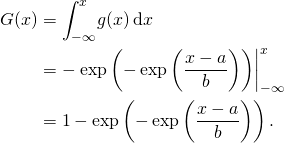
Durch Umstellen nach ![]() erhalten wir die Quantilfunktion
erhalten wir die Quantilfunktion ![]() , die wir später zur Erzeugung der sogenannten QQ Plots benötigen:
, die wir später zur Erzeugung der sogenannten QQ Plots benötigen:
![]()
Vorteile / Nachteile:
Eine zwei-parametrige Dichtefunktion ![]() hat bei kleineren Datensätzen den Vorteil, dass Effekte einer Überanpassung (engl. overfitting) nicht so deutlich werden.
hat bei kleineren Datensätzen den Vorteil, dass Effekte einer Überanpassung (engl. overfitting) nicht so deutlich werden.
Auf der anderen Seite haben zwei-parametrige Dichtefunktionen ganz allgemein den Nachteil eines schlechteren Anpassungsverhaltens, so dass charakteristische Merkmale der empirischen Messreihe gegebenenfalls nicht korrekt abgebildet werden.
Anpassung der Dichte der Gumbel-Verteilung für die Minima
Da bei der Anpassung der Dichte ![]() an die minimalen Werte des Stiftungsvermögens der Formparameter
an die minimalen Werte des Stiftungsvermögens der Formparameter ![]() ungefähr Null war, wurde eine erneute Anpassung an die speziellere Gumbel-Dichte
ungefähr Null war, wurde eine erneute Anpassung an die speziellere Gumbel-Dichte ![]() durchgeführt.
durchgeführt.
Mit der Momentenmethode und der (logarithmierten) Maximum-Likelihood-Methode erfolgte die Anpassung an die zehn Vermögensminima, so dass sich zwei Paare von Verteilungsparametern für Lage und Streuung auflisten lassen.
Bemerkung: Speziell zur Maximum-Likelihood-Methode vergleiche auch den Beitrag Parameterschätzung bei der Gumbel-Verteilung.
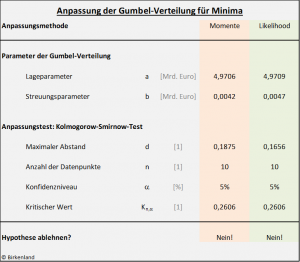
Die nachfolgende Tabelle fast die Ergebnisse zusammen.
Wie wir sehen, führen beide Methoden auf leicht unterschiedliche Werte für Lage- und Streuungsparameter der Gumbel-Verteilung.
Im Folgenden muss nun entschieden werden, welcher Parametersatz geeigneter ist, um die Messdaten zu beschreiben.
Anpassungsgüte
Bei einer geringen Anzahl an Messdaten (hier: zehn Minima) kann die Anpassungsgüte z. B. mit dem einfach handhabbaren Kolmogorow-Smirnow-Test abgeschätzt werden.
Dieser Test wurde für das Beispiel des Stiftungsvermögens durchgeführt.
Zu beachten ist, dass der Ablehnungsbereich der Nullhypothese – die Minima entstammen einem Zufallsprozess dem eine Gumbel-Verteilung zu Grunde liegt – bei diesem Test durch einen kleineren kritischen Wert ![]() abgegrenzt wird, als in der Standardliteratur tabelliert.
abgegrenzt wird, als in der Standardliteratur tabelliert.
Die Besonderheit bei der vorliegenden Analyse ist nämlich, dass der Lage- und der Streuungsparameter der Gumbel-Verteilung ebenfalls aus den Daten bestimmt werden mussten.
Dieser Umstand führt dazu, dass die kritischen Werte des Kolmogorow-Smirnow-Tests von der angenommenen Verteilung abhängig werden und sich auf rund ![]() verkleinern, vgl. hierzu die Aufsätze von Michael A. Stephens.
verkleinern, vgl. hierzu die Aufsätze von Michael A. Stephens.
Wie ein Vergleich des maximalen Abstands ![]() (Testgröße des Kolmogorow-Smirnow-Tests) mit dem kritischen Wert
(Testgröße des Kolmogorow-Smirnow-Tests) mit dem kritischen Wert ![]() zeigt, ist im Ergebnis festzustellen, dass auf dem gewählten Konfidenzniveau von 5 % die Nullhypothese nicht abzulehnen ist, vgl. auch unten den Anhang (b) dieses Artikels.
zeigt, ist im Ergebnis festzustellen, dass auf dem gewählten Konfidenzniveau von 5 % die Nullhypothese nicht abzulehnen ist, vgl. auch unten den Anhang (b) dieses Artikels.
Insgesamt liefern im vorliegenden Fall beide Parameterschätzverfahren näherungsweise ähnliche Schätzungen für den Lage- und den Streuungsparameter.
Die logarithmierte Maximum-Likelihood-Methode liefert jedoch Verteilungsparameter, die im Anpassungstest zu einer etwas besseren Güte führen.
PP und QQ Plots
Optisch kann das Ergebnis auch anhand von PP bzw. QQ Plots überprüft werden.
Vereinfacht ausgedrückt verdeutlichen die Plots folgende Sachverhalte:
- PP Plots stellen die Wahrscheinlichkeiten der empirischen Verteilungsfunktion gegenüber denen der geschätzten, theoretischen Verteilungsfunktion dar.
- QQ Plots stellen die Quantile der empirischen Verteilungsfunktion gegenüber denen der geschätzten, theoretischen Verteilungsfunktion dar.
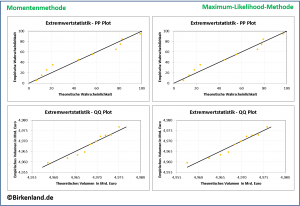
Die folgende Grafik zeigt die Plots für die Momenten- und die logarithmierte Maximum-Likelihood-Methode.
Die relative Lage der einzelnen Punkte (orange) gegenüber den eingezeichneten Diagonalen (schwarz) dient als optisches Kriterium für die Güte der Anpassung.
In beiden Plots gilt die einfache Überlegung: Je näher die Punkte sich an die Diagonale anschmiegen, umso besser ist die Anpassung.
Im Ergebnis kann auch hier festgestellt werden, dass beide Methoden zur Parameterschätzung akzeptable Ergebnisse liefern.
Es gibt lediglich kleinere Unterschiede in den Grafiken.
Zu erkennen ist, dass sich im Fall der logarithmierten Maximum-Likelihood-Methode die Punkte besser an die Diagonale anschmiegen.
Einfach ausgedrückt: Die jeweiligen Diagonalen verlaufen bei der logarithmierten Maximum-Likelihood-Methode mehr durch die Mitte der Punktewolke.
Abschließende Bewertung der Anpassung
Sowohl der Kolmogorow-Smirnow-Test als auch die optische Überprüfung der PP und QQ Plots legen nahe, dass die Verteilung der Vermögensminima in dem hier analysierten Fall mit großer Sicherheit durch die Gumbel-Verteilung beschrieben wird.
Die logarithmierte Maximum-Likelihood-Methode führt bei der Anpassung zu Verteilungsparametern, die etwas geeigneter scheinen.
Daher wird die Gumbel-Verteilung für die Minima mit diesen Lage- und Streuungsparametern im Folgenden weiter untersucht.
Ergebnisse der Anpassung
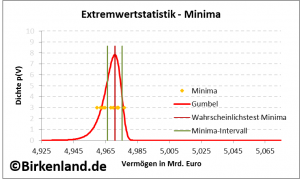
Die folgende Grafik zeigt mit dem roten Graphen die Anpassung der Gumbel-Dichte ![]() an die zehn Minima (orange).
an die zehn Minima (orange).
Aufgetragen ist die Gumbel-Dichte (rot; in willkürlichen Einheiten) über dem Stiftungsvermögen in Euro.
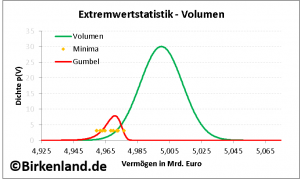
Abbildung 3: Darstellung der Dichte für die wöchentlichen Volumensveränderungen (grün) und die jährlichen Minima (rot). Die Punkte (orange) zeigen die Lage der Minima der letzten zehn Jahre.
Die Abbildung 3 zeigt außerdem die Dichte der Verteilung des Stiftungsvermögens (grün) um den zentralen Wert von 5 Mrd. Euro.
Es handelt sich hierbei um eine Normalverteilung, die den zentralen Wert von 5 Mrd. Euro als Lageparameter besitzt.
Ausgehend von dem Stiftungsvermögen von 5 Mrd. Euro kann am Wochenschluss das Vermögen gemäß der grün eingezeichneten Dichte irgendwo innerhalb einer Bandbreite von etwa 4,94 Mrd. Euro bis 5,06 Mrd. Euro liegen.
Die Dichte der Gumbel-Verteilung (rot) überdeckt in der Abbildung 3 einen bestimmten Wertebereich des Stiftungsvermögens und markiert damit die möglichen Lagen des minimalen Vermögenswertes im nächsten Kalenderjahr.
Daraus folgt der Schluss: Wenn im nächsten Kalenderjahr ein minimales Stiftungsvermögen auftritt, dann liegt dieses mit hoher Wahrscheinlichkeit irgendwo in der Bandbreite zwischen 4,94 Mrd. Euro und 4,98 Mrd. Euro.
Bemerkung: Statistisch betrachtet liegen die Normalverteilung, sowie auch die Exponentialverteilung, die Gammaverteilung und die logarithmische Normalverteilung im Anziehungsbereich der Gumbel-Verteilung.
Salopp formuliert, besitzen die vorgenannten vier Verteilungen die Gumbel-Verteilung als Grenzverteilung für die Extrema.
Da die Verteilung der Wochenwerte des Stiftungsvermögens einer Normalverteilung (grün) entspricht, ist somit die Grenzverteilung der Extremwerte eine Gumbel-Verteilung (rot).
Erwartungswert und Varianz
Bei der Risikobewertung im Rahmen des Portfoliomanagements können mit der Dichte einer Verteilung weitere Kenngrößen abgeleitet werden. Zwei davon – Erwartungswert und Varianz – sind dabei von besonderem Interesse.
Für eine allgemeine Dichtefunktion ![]() sind der Erwartungswert und die Varianz durch folgende Integrale gegeben:
sind der Erwartungswert und die Varianz durch folgende Integrale gegeben:
![Rendered by QuickLaTeX.com \begin{flalign*} \text{E}[x] & = \int_{-\infty}^{\infty} x f(x) \, \mathrm dx \\ \text{Var}[x] & = \int_{-\infty}^{\infty} \left(x -\text{E}[x] \right)^2 f(x) \, \mathrm dx \\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-3af20456ad5c5e5afaa230a89ae8c696_l3.png)
Der Erwartungswert und die Varianz der Gumbel-Verteilung für Maximalwerte können damit berechnet werden und stehen mit den Parametern ![]() und
und ![]() der Dichte in folgendem Zusammenhang:
der Dichte in folgendem Zusammenhang:
![Rendered by QuickLaTeX.com \begin{flalign*} \text{E}[x] & = a + b \gamma \\ \text{Var}[x] & = \frac{\pi^2 b^2}{6} \\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-7961ce8a6860d32aaab72fa2cde48dd8_l3.png)
Hierbei ist ![]() die Euler-Mascheroni-Konstante.
die Euler-Mascheroni-Konstante.
Für die Dichte der Gumbel-Verteilung sind – abhängig von Lage- und Streuungsparameter – die statistischen Kenngrößen Erwartungswert und Varianz somit analytisch gegeben.
Wird die oben definierte Koordinatentransformation ![]() durchgeführt und anschließend wieder
durchgeführt und anschließend wieder ![]() durch
durch ![]() ersetzt, so berechnet sich der Erwartungswert und die Varianz der Gumbel-Verteilung
ersetzt, so berechnet sich der Erwartungswert und die Varianz der Gumbel-Verteilung ![]() für Minimalwerte wie folgt:
für Minimalwerte wie folgt:
![Rendered by QuickLaTeX.com \begin{flalign*} \text{E}[x] & = a - b \gamma \\ \text{Var}[x] & = \frac{\pi^2 b^2}{6} \\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-b7c5232562986bbc85d1a51c1138f015_l3.png)
Während die Varianz bei einer Verschiebung gleich bleibt, wechselt bei dem Erwartungswert lediglich das Vorzeichen vor dem zweiten Ausdruck.
Die folgende Abbildung zeigt die an die empirischen Daten der Stiftung angepasste Dichte der Gumbel-Verteilung (rot) noch einmal vergrößert.
Dargestellt ist zusätzlich wieder die Lage der Minima des Stiftungsvermögens (orange) in den vergangenen zehn Kalenderjahren.
Der Vermögenswert von etwa 4,971 Mrd. Euro markiert das wahrscheinlichste Minimum (mathematisch: der Modalwert der Dichte) des Stiftungsvermögens (weinrot) und ist gleichzeitig der Lageparameter ![]() der Verteilung.
der Verteilung.
Aus der Anpassung der Gumbel-Verteilung an die zehn Minima des Stiftungsvermögens folgte neben dem Lageparameter auch der Streuungsparameter ![]() .
.
Im vorliegenden Fall hat der Streuungsparameter den Wert von etwa 0,005 Mrd. Euro.
In der Abbildung 3 ist der durch den Streuungsparameter bemessene Streubereich symmetrisch um den Lageparameter mit den hellgrünen Strichen verdeutlicht.
Aus den Parametern ![]() und
und ![]() der Dichte lassen sich mit den zuvor abgeleiteten Formeln der Erwartungswert zu 4,968 Mrd. Euro und die Standardabweichung als Wurzel der Varianz zu 0,006 Mrd. Euro berechnen.
der Dichte lassen sich mit den zuvor abgeleiteten Formeln der Erwartungswert zu 4,968 Mrd. Euro und die Standardabweichung als Wurzel der Varianz zu 0,006 Mrd. Euro berechnen.
Dieses Ergebnis kann vereinfacht wie folgt interpretiert werden: Wird im kommenden Kalenderjahr ein Vermögensminimum registriert, so liegt dieses Minimum mit großer Wahrscheinlichkeit in dem Bereich zwischen 4,962 Mrd. Euro und 4,974 Mrd. Euro um den Erwartungswert von 4,968 Mrd. Euro.
Nebenrechnung:
4,962 Mrd. Euro = (4,968 – 0,006) Mrd. Euro
4,974 Mrd. Euro = (4,968 + 0,006) Mrd. Euro
Die folgenden Überlegungen geben Antwort auf die Frage: Wie groß ist diese Wahrscheinlichkeit?
Die Auswertung des Integrals
![]()
liefert für eine beliebige Dichte ![]() die Wahrscheinlichkeit
die Wahrscheinlichkeit ![]() , dass der Wert
, dass der Wert ![]() eines Zufallsprozesses innerhalb des Wertebereichs zwischen
eines Zufallsprozesses innerhalb des Wertebereichs zwischen ![]() und
und ![]() für
für ![]() liegt.
liegt.
Für das Stiftungsvermögen ergibt diese Auswertung eine Wahrscheinlichkeit von etwa 70 %, dass ein künftiges minimales Stiftungsvermögen innerhalb des Streubereichs mit den Eckwerten ![]() 4,962 Mrd. Euro und
4,962 Mrd. Euro und ![]() 4,974 Mrd. Euro liegt.
4,974 Mrd. Euro liegt.
Extremwertstatistik im Portfoliomanagement: Risikobewertung im Risikoreport
Auf Basis der zuvor abgeleiteten Ergebnisse würde die Prognose des minimalen Stiftungsvermögens im kommenden Kalenderjahr den Erwartungswert der Minima im Rahmen der Risikobetrachtung zu Grunde legen.
Im Risikoreport des Portfoliomanagers für das Stiftungsvermögen könnte im einfachsten Fall somit folgende Formulierung stehen:
Wenn im kommenden Jahr ein minimales Vermögen auftritt, dann dürfte es in der Nähe des Erwartungswertes bei etwa 4,968 Mrd. Euro liegen.
Abhängig davon, ob der Erwartungswert der Minima im Einklang mit den Vorgaben in den Anlagerichtlinien steht oder nicht, muss gegebenenfalls die Zusammensetzung des Portfolios neu gestaltet werden.
Anhang
(a) Von der Gompertz-Verteilung zur Gumbel-Verteilung
Die Gompertz-Verteilung spielt in der Versicherungswirtschaft, bei demografischen Bewertungen, in der Biologie und der Gerontologie eine große Rolle.
Im Wesentlichen werden mit der Gompertz-Verteilung Lebensspannen statistisch beschrieben.
Die Verteilung zählt zu den zwei-parametrigen Verteilungsfunktionen und hat folgende Gestalt:
![]()
Der Parameter ![]() wird als Formparameter bezeichnet und
wird als Formparameter bezeichnet und ![]() ist in dieser Verteilung der Streuungsparameter.
ist in dieser Verteilung der Streuungsparameter.
Wir wollen jetzt zeigen, wie die Gumbel-Verteilung aus der Gompertz-Verteilung hergeleitet werden kann und somit ein Spezialfall der letzteren Verteilung ist.
Den Formparameter ![]() können wir mit einem neuen Parameter
können wir mit einem neuen Parameter ![]() in die Darstellung
in die Darstellung
![]()
überführen.
Diesen Ausdruck setzen wir in die Gompertz-Verteilung ein und erhalten:
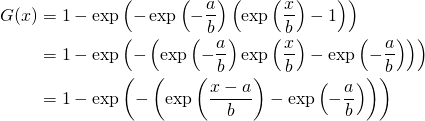
In dem letzten Ausdruck wird ersichtlich, dass der Parameter ![]() die Funktion eines Lageparameters hat.
die Funktion eines Lageparameters hat.
Wird davon ausgegangen, dass ![]() sehr viel größer als
sehr viel größer als ![]() ist, also das gilt
ist, also das gilt ![]() . Dann wird der Quotient
. Dann wird der Quotient ![]() sehr groß und der Wert des Terms
sehr groß und der Wert des Terms ![]() geht gegen Null.
geht gegen Null.
Diese Annahme ist bei dem Beispiel des Stiftungsvermögens gerechtfertigt, weil der Lageparameter ![]() in der Größenordnung von 5 Mrd. Euro liegt und der Streuungsparameter
in der Größenordnung von 5 Mrd. Euro liegt und der Streuungsparameter ![]() etwa Werte im Bereich von 0,005 Mrd. Euro annimmt.
etwa Werte im Bereich von 0,005 Mrd. Euro annimmt.
Damit gilt in dem Stiftungsbeispiel: ![]() .
.
Durch streichen des Terms ![]() erhalten wir schließlich die Darstellung der Gumbel-Verteilung für Minima:
erhalten wir schließlich die Darstellung der Gumbel-Verteilung für Minima:
![]()
(b) Kritische Werte 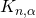 für den Kolmogorow-Smirnow-Test
für den Kolmogorow-Smirnow-Test
Werden die Parameter der Gumbel-Verteilung geschätzt, so können für den Gütetest nach Kolmogorow und Smirnow nicht die üblichen tabellierten kritischen Werte ![]() genutzt werden.
genutzt werden.
Ablehnungs- und Annahmebereich für die Nullhypothese werden in diesem Fall durch kritische Werte getrennt, die rund ![]() kleiner als die standardmäßig tabellierten Werte sind.
kleiner als die standardmäßig tabellierten Werte sind.
Darüber hinaus sind die kritischen Werte abhängig von der zugrundeliegenden Verteilungsfunktion und im Allgemeinen nicht analytisch berechenbar.
Monte-Carlo-Simulationen liefern Tabellen der kritischen Werte abhängig von der Verteilungsfunktion, wenn die Parameter der Verteilungsfunktion ebenfalls aus den vorliegenden Daten geschätzt werden müssen.
Für die Anwendung der Extremwertstatistik im Portfoliomanagement sind die vorliegenden Datenreihen für die Extremwerte in der Regel sehr kurz. Von besonderem Interesse sind daher kritische Werte für 4 bis 20 Datenpunkte.
Für den Fall der angepassten Gumbel-Verteilung für Minima wurden eigene Monte-Carlo-Simulationen durchgeführt, um die kritischen Werte des Anpassungstests zu tabellieren.
Chandra et al. hat 1981 die kritischen Werte für zehn und zwanzig Datenpunkte angegeben.
Die hier simulierten Werte für zehn und zwanzig Datenpunkte entsprechen im Rahmen einer Genauigkeit von ![]() 0,001 den von Chandra et al. angegebenen Werten.
0,001 den von Chandra et al. angegebenen Werten.
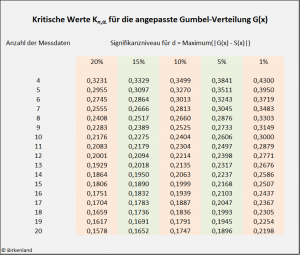
Die nachfolgende Tabelle zeigt die kritischen Werte ![]() des Kolmogorow-Smirnow-Tests bei angepasster Gumbel-Verteilung.
des Kolmogorow-Smirnow-Tests bei angepasster Gumbel-Verteilung.
Monte-Carlo-Simulation
Es wurden für jede in der Tabelle notierte Anzahl ![]() von Datenpunkten jeweils 500.000 Monte-Carlo-Simulationen durchgeführt.
von Datenpunkten jeweils 500.000 Monte-Carlo-Simulationen durchgeführt.
In jedem einzelnen Monte-Carlo-Simulationsschritt sind ![]() Datenpunkte mit einer Gumbel-Verteilung erzeugt worden. Die Verteilungsparameter waren dabei zwar bekannt, blieben aber für die weiteren Analysen ungenutzt.
Datenpunkte mit einer Gumbel-Verteilung erzeugt worden. Die Verteilungsparameter waren dabei zwar bekannt, blieben aber für die weiteren Analysen ungenutzt.
Stattdessen wurde jedes Mal eine Anpassung an die ![]() erzeugten Datenpunkten vorgenommen und dabei der Lage- und der Streuungsparameter einer Gumbel-Verteilung
erzeugten Datenpunkten vorgenommen und dabei der Lage- und der Streuungsparameter einer Gumbel-Verteilung ![]() berechnet.
berechnet.
Die Anpassung erfolgte mit Hilfe der logarithmierten Maximum-Likelihood-Methode.
Des Weiteren erfolgte eine Berechnung der empirischen Verteilungsfunktion ![]() aus den Datenpunkten.
aus den Datenpunkten.
Das Ergebnis jedes Simulationsschritts war der maximale Abstand ![]() zwischen der angepassten Gumbel-Verteilung
zwischen der angepassten Gumbel-Verteilung ![]() und der empirischen Verteilungsfunktion
und der empirischen Verteilungsfunktion ![]() .
.
Pro Anzahl ![]() an Datenpunkten sind somit 500.000 maximale Abstandswerte
an Datenpunkten sind somit 500.000 maximale Abstandswerte ![]() zufällig erzeugt worden.
zufällig erzeugt worden.
Aus der aufsteigend sortierten Reihe der maximalen Abstände ![]() sind zu den entsprechenden Konfidenzniveaus, sodann die kritischen Werte entnommen worden.
sind zu den entsprechenden Konfidenzniveaus, sodann die kritischen Werte entnommen worden.
Interpretation des Kolmogorow-Smirnow-Tests
Die Nullhypothese wird zu einem Konfidenzniveau ![]() bei einer Länge der Datenreihe von
bei einer Länge der Datenreihe von ![]() Punkten abgelehnt, wenn die Testgröße
Punkten abgelehnt, wenn die Testgröße ![]() des Kolmogorow-Smirnow-Tests größer als der entsprechende kritische Wert
des Kolmogorow-Smirnow-Tests größer als der entsprechende kritische Wert ![]() ist.
ist.
Beispiel: Stiftungsvermögen
Im Beispiel des Stiftungsvermögens lagen zehn Minima zur Anpassung der Gumbel-Verteilung vor, d. h. ![]() .
.
Als Konfidenzniveau war ![]() vorgegeben.
vorgegeben.
Aus der obigen Tabelle ergibt sich somit ein kritischer Wert von ![]() 0,2606.
0,2606.
Die mit der Momentenmethode angepasste Gumbel-Verteilung führte in diesem Beispiel auf einen maximalen Abstand von ![]() 0,1875. Vergleiche hierzu auch die Ergebnistabelle im Haupttext.
0,1875. Vergleiche hierzu auch die Ergebnistabelle im Haupttext.
Mit dem Ergebnis ![]() folgt, dass die Nullhypothese – die Minima entstammen einem Zufallsprozess dem eine Gumbel-Verteilung zu Grunde liegt – nicht abgelehnt werden sollte.
folgt, dass die Nullhypothese – die Minima entstammen einem Zufallsprozess dem eine Gumbel-Verteilung zu Grunde liegt – nicht abgelehnt werden sollte.
Weiterführende Literaturquellen zur Extremwertstatistik
Extremwerttheorie
http://wwwmath.uni-muenster.de/statistik/kabluchko/Skripte/Skript_Extremwerttheorie.pdf
Extremwertstatistik zur Modellbildung
Modelling Extremal Events: for Insurance and Finance
(Embrecht, Klüppelberg, Mikosch im Springer-Verlag, 2001)
Theorie der Extremwertstatistik
https://wwwmath.uni-muenster.de/statistik/loewe/extrem.pdf
Über die Extremwertstatistik und Wiederkehrintervalle in langzeitkorrelierten Systemen
http://www.physik.uni-halle.de/Fachgruppen/kantel/PhD_Eichner.pdf
Ermittlung des Value-at-Risk von Finanzportefeuilles mit Methoden der Extremwertstatistik
http://www.risknet.de/fileadmin/eLibrary/Extremwerttheorie-Diplomarbeit-Frahm.pdf