Definition eines Schätzers für die Korrelation im Rahmen des optimalen Risikomanagements

Vorgestellt wird ein auf statistischen Methoden beruhendes Verfahren, um die Korrelation vor dem Hintergrund einer Risikopräferenz mit Hilfe eines neuen Schätzers zu berechnen.

Beim Risikomanagement in einer Bank führt dieser neue Korrelationsschätzer bspw. dazu, dass zwei unterschiedliche Bewertungsansätze in einem vereinheitlichten Rahmen auf Basis statistischer Methoden zu einem Bewertungsansatz gelangen.

Grundlage für das nachstehend beschriebene Verfahren ist der Aufsatz: On biased correlation estimation.

Einleitung

Das Gesamtrisiko der Eigenanlage einer Bank setzt sich aus verschiedenen Risikoarten zusammen. Unterschieden werden z.B.: das Kreditausfallrisiko, das Marktpreisrisiko, das Zinsrisiko und das Bonitätsrisiko.

Bei der Zusammenfassung von verschiedenen Risiken zu einem Gesamtrisiko ist die Berücksichtigung von gegenseitigen Abhängigkeiten möglich.

Diese Abhängigkeiten können formal durch den so genannten Korrelationskoeffizienten $\rho$ (kurz: die Korrelation) quantifiziert werden. Die Korrelation nimmt ausschließlich Werte zwischen $-1$ und $+1$ an.

Bei der Vermögensanlage einer Bank wird u.a. das Ziel verfolgt, durch Verteilung des Kapitals auf verschiedene Vermögenswerte eine möglichst hohe Rendite zu erwirtschaften. Als Vermögenswerte können bspw. Aktien, Anleihen, Immobilien oder Rohstoffe gekauft werden.

Mit einem bestimmten Vermögenswert ist dabei ein entsprechendes Einzelrisiko verbunden, dass sich durch die Volatilität $\sigma$ (Wertschwankung) quantifizieren lässt.

Bei einem Portfolio, das aus zwei Vermögenswerten (A und B) besteht, lässt sich nach Markowitz das Gesamtrisiko des Portfolios $\sigma^2_{PF}$ wie folgt berechnen:

(1) $\begin{eqnarray*} \sigma^2_{PF}&=& w_A^2 \sigma_A^2 + w_B^2 \sigma_B^2 + 2 w_A w_B \sigma_A \sigma_B \times \rho \end{eqnarray*}$

Mit $w_A$ und $w_B$ sind die prozentualen Gewichte bezeichnet, die sich zu $100 \%$ addieren.

Der Ertrag des Portfolios $R_{PF}$ berechnet sich über die gewichtete Summe der einzelnen Ertragserwartungen $R_A$ und $R_B$ :

(2) $\begin{eqnarray*} R_{PF}&=& w_A\; R_A + w_B \; R_B \end{eqnarray*}$

Die Aufteilung des Vermögens ( $w_A$ und $w_B$ ) resultiert aus einer Optimierung und erfolgt z.B. so, dass zu vorgegebenem Ertrag ein minimales Risiko bestimmt wird.

Da i.A. der genaue Wert der Korrelation $\rho$ nicht bekannt ist, muss in der Praxis ein Schätzer für die Korrelation $\hat r$ ausgewählt werden, um Einzelrisiken zu einem Gesamtrisiko zusammenfassen zu können.

Die Auswahl eines Schätzers $\hat r$ für die Korrelation lässt sich im Rahmen der Statistik unterschiedlich interpretieren. Die Qualität von Schätzern wird dabei präzise definiert und bspw. durch systematische und unsystematische Fehler klassifiziert.

Exkurs: Der statistische Gesamtfehler der Korrelation setzt sich aus zwei Teilen zusammen. Der erste Teil beschreibt den so genannten systematischen Fehler (Verzerrung, Bias), der sich in einer systematischen Verschiebung des Schätzwertes zeigt. Der zweite Anteil beschreibt den unsystematischen Fehler, der aufgrund der empirischen Streuung bei der Schätzung zu berücksichtigen ist. Sowohl der systematische als auch der unsystematische Fehler der Korrelation haben Einfluss auf die Optimierung.

Abhängig von der Zielstellung sind verschiedene Herangehensweisen zur Wahl eines Schätzers für die Korrelation möglich. In einer Bank werden hierzu im Wesentlichen zwei Richtungen unterschieden:

Controlling: Der Korrelationsschätzer wird im (Risiko-)Controlling oft zu 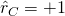$\hat r_C = +1$ gewählt und erfüllt die Forderung, dass eine Unterschätzung der Korrelation aufgrund der empirischen Streuung nicht vorkommen darf. Denn Letzteres würde ggf. zu einem Unterschätzen des Gesamtrisikos führen. Der systematische Fehler bleibt hingegen unberücksichtigt.

Treasury: Der Korrelationsschätzer ist hier der Likelihood-Schätzer. Somit gilt 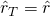$\hat r_T = \hat r$ , vgl. hierzu auch Gleichung (3). Dieser Schätzer erfüllt die Forderung, dass der statistische Gesamtfehler minimiert wird.

Im Folgenden wird ein praxisorientiertes Beispiel für ein vorgegebenes Risiko $\sigma_0 = 5\%$ betrachtet. Das bedeutet, dass das Gesamtrisiko bei der Verteilung des Vermögens auf die zwei Vermögenswerte (A und B) höchstens $\sigma_0$ betragen darf.

Die Abbildung 1 zeigt exemplarisch die Situation des Treasuries und des Controllings am Beispiel der zwei Vermögenswerte. Das gezeigte Risiko-Ertragsdiagramm stellt den Ertrag gegenüber dem Gesamtrisiko dar.

In der Grafik werden drei Effizienzlinien zu unterschiedlichen Korrelationsschätzern dargestellt:

Aus der Sicht des Controllings ( $\hat r_C=+1.0$ ),
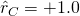des Treasuries ( 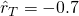$\hat r_T=-0.7$ ) und
beispielsweise für einen Kompromiss ( $\hat r = +0.5$ ).

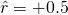Im Fall des Controllings wäre ein Portfolio optimal, dass eine Rendite von etwa $4.5\%$ erwarten lässt (A).

Im Fall des Treasuries würde bei gleicher Portfoliogewichtung ein deutlich geringeres Risiko ausgewiesen werden (B).

Bei gleichem vorgegebenem Risiko könnte der Treasurer eine andere Gewichtung der Vermögenswerte vornehmen und einen höheren Ertrag erwarten (C).

Für die Korrelation $\hat r = +0.5$ schneidet die Effizienzlinie die jeweiligen Verbindungsgraden (gestrichelt) in den Punkten D und E.

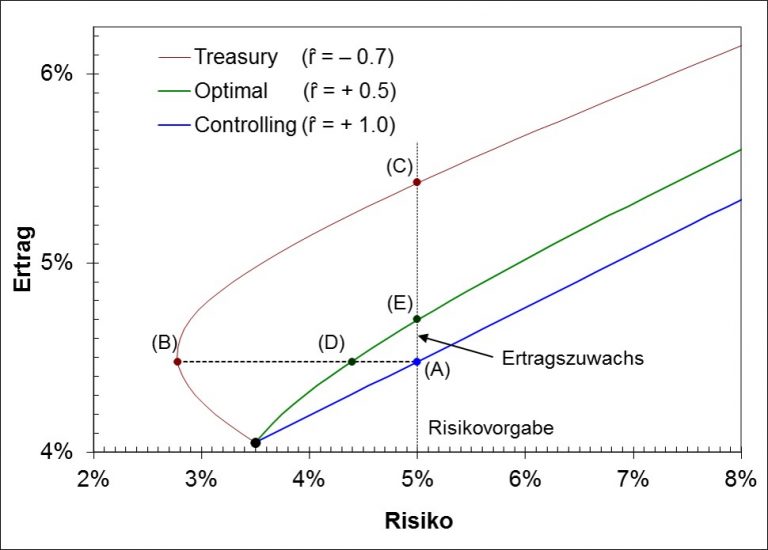
Abbildung 1: Beispiel eines Risiko-Ertragsdiagramms mit drei Effizienzlinien für unterschiedliche Korrelationen.

Das Portfolio am Punkt E lässt bei vorgegebenem Risiko gegenüber dem Portfolio am Punkt A einen Ertragszuwachs erwarten.

Für den Entscheider entsteht daher ein Zielkonflikt bezüglich der Risikomessung und damit auch der Aufteilung des Vermögens (Controlling- vs. Treasury-Portfolioempfehlung).

Zur Lösung dieses Zielkonfliktes wird im Folgenden ein Verfahren vorgestellt, welches eine differenzierte und systematische Beurteilung der Situation ermöglicht.

Das Verfahren basiert auf der Definition eines neuen Schätzers $\rho_\alpha$ für die Korrelation. Dieser bietet die Möglichkeit für einen Kompromiss zwischen den beiden unterschiedlichen Sichtweisen von Controlling und Treasury.

Ausgangspunkt bildet die Überlegung, dass der Standardschätzer des Treasuries eine Zufallszahl ist – die einer Wahrscheinlichkeitsverteilung $P$ mit zugehöriger Wahrscheinlichkeitsdichte $p$ gehorcht – und der errechnete Wert lediglich eine Realisierung darstellt.

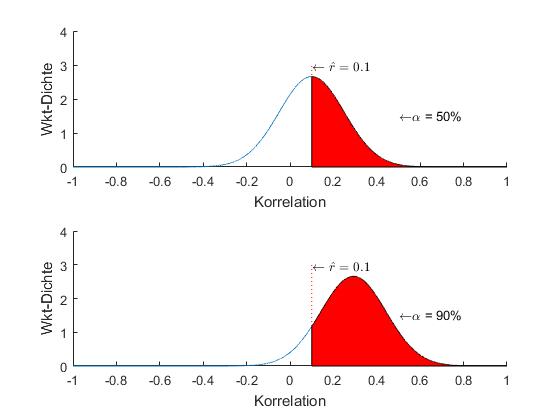
Um nun zu einem neuen Schätzer für die Korrelation zu gelangen, wird der Standardschätzer des Treasuries mit einer Wahrscheinlichkeit $\alpha$ bewertet und als Quantil der – noch zu bestimmenden – Wahrscheinlichkeitsverteilung betrachtet, vgl. Abbildung 2.

Es wird also davon ausgegangen, dass andere Realisierungen der Zufallszahl mit einer Wahrscheinlichkeit von $\alpha$ oberhalb des errechneten Standardschätzers liegen. Der just beobachtete Korrelationswert also die Grenze zu den $1-\alpha$ kleineren Korrelationen darstellt.

Die Wahrscheinlichkeit $\alpha$ drückt somit das Misstrauen des Controllings in den Standardschätzer des Treasuries aus. Die Wahrscheinlichkeit $\alpha = 100\%$ bedeutet dabei höchstes Mißtrauen (worst case).

Durch Vorgabe des Quantils – hier der Standardschätzer des Treasuries – zur Wahrscheinlichkeit $\alpha$ ist die Lage der Wahrscheinlichkeitsdichte $p$ eindeutig gegeben und es lässt sich dann der neue Schätzer $\rho_\alpha$ für die Korrelation berechnen.

Von besonderem Interesse sind dabei die Quantile für $\alpha \lesssim 100\%$ , da diese das Verhalten in der Nähe der gewöhnlichen worst case Annahme des Controllings beschreiben.

Wird dem Standardschätzer des Treasuries aus Sicht des Controllings ein gewisses Vertrauen ( $\alpha < 100\%$ ) entgegengebracht, dann liefert das nachfolgend detailliert dargestellte Verfahren einen eindeutigen Wert $\rho_\alpha$ als neuen Schätzer für die Korrelation.

Mit dieser Korrelation verbunden ist eine Effizienzlinie, die in Abbildung 1 durch die Punkte D und E verläuft.

Korrelationsschätzer und Wahrscheinlichkeitsdichte

Sei $(x_1, y_1), \ldots, (x_n, y_n)$ eine unabhängig, bivariat verteilte Stichprobe vom Umfang $n$ .

Dann lässt sich der statistische Schätzer $\hat r$ für die unbekannte wahre Korrelation $\rho$ (Parameter der Wahrscheinlichkeitsverteilungsfunktion) wie folgt berechnen:

(3) $\begin{eqnarray*} \hat r = \frac{\sum_{i=1}^n (x_i - \hat\mu_x)(y_i - \hat\mu_y)}{\sqrt{\sum_{i=1}^n (x_i - \hat\mu_x)^2\sum_{i=1}^n (y_i - \hat\mu_y)^2}} \end{eqnarray*}$

Mit $\hat\mu$ sind die Schätzer der Mittelwerte der jeweiligen Messreihe bezeichnet, bspw. ist $\hat\mu_x=1/n \sum_{i=1}^n x_i$ .

Der mit der Gleichung (3) bestimmte Wert wird auch als empirischer Korrelationskoeffizient bezeichnet und ist in der Praxis weit verbreitet. Er findet u.a. im Bereich des Treasuries als Standardschätzer Anwendung, d.h. es gilt: $\hat r_T = \hat r$ .

Die Wahrscheinlichkeitsdichte für die empirische Korrelation $\hat r$ ist in der Literatur gegeben durch

(4) $\begin{eqnarray*} p(r|\rho, n)&=& \frac{2^{n-3}}{\pi\Gamma(n-1)}(1-\rho^2)^{\frac{n-1}{2}} (1-r^2)^{\frac{n-4}{2}} \nonumber \\ & & \times\; \sum_{k=0}^\infty\Gamma^2\left(\frac{n+k-1}{2} \right) \frac{(2\rho r)^k}{k!} \end{eqnarray*}$

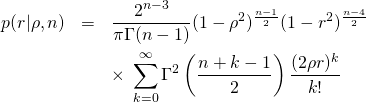
für $n\ge 2$ .

In Gleichung (4) bedeutet $\Gamma(x)$ die Euler-Gamma-Funktion und $\rho$ als Verteilungsparameter entspricht im Grenzfall $n\rightarrow\infty$ der wahren Korrelation.

Die Wahrscheinlichkeitsdichte ist für jeden Stichprobenumfang $n\ge 2$ normiert:

(5) $\begin{eqnarray*} \int_{-1}^{+1} p(r|\rho, n)\, dr = 100\%. \end{eqnarray*}$

Schätzer für die Korrelation gemäß Risikopräferenz

Das hier beschriebene Verfahren zur Bestimmung eines Korrelationsschätzers soll erreichen, dass eine Unterschätzung der Korrelation und damit eine Unterschätzung des Gesamtrisikos bei Bedarf vermieden wird.

In der Praxis kann dem empirische Schätzer $\hat r$ für die Korrelation ein mehr oder weniger großes Misstrauen entgegengebracht werden.

Die Abbildung 2 verdeutlicht die Situation für zwei Fälle.

In der oberen Grafik für $\alpha = 50 \%$ liegen mögliche weitere Realisierungen der Zufallszahl gleich anteilig links und rechts vom errechneten Wert der Korrelation $\hat r = 0.1$ .

In der unteren Grafik liegen $\alpha = 90 \%$ der möglichen weiteren Realisierungen der Zufallszahl oberhalb des errechneten Werts der Korrelation.

Abbildung 2: Abhängigkeit der Lage der Wahrscheinlichkeitsdichte von der Wahrscheinlichkeit $\alpha$ .

Auf Basis der Wahrscheinlichkeit $\alpha$ und des errechneten Werts der Korrelation $\hat r$ (empirischer Schätzer) ist es möglich, einen neuen Schätzer $\rho_\alpha$ zu bestimmen.

Ausgangspunkt dazu bildet die Wahrscheinlichkeitsdichte (4).

Mit dem empirischen Schätzwert $\hat r$ aus Gleichung (3) und dem Stichprobenumfang $n$ ist die gesuchte Korrelation $\rho_\alpha$ durch die Gleichung:

(6) $\begin{eqnarray*} \alpha = \int_{\hat r}^{1} p(r|\rho_\alpha, n)\, dr \end{eqnarray*}$

eindeutig bestimmt.

Das bedeutet, der mit Gleichung (3) geschätzte Korrelationswert $\hat r$ wird als $(1-\alpha)$ -Quantil der Verteilung $p(r|\rho_\alpha, n)$ interpretiert.

Aus der impliziten Integralgleichung (6) wird dann der Verteilungsparameter $\rho_\alpha$ als neuer Korrelationsschätzer bestimmt.

Aufgrund der Monotonieeigenschaft der Verteilungsfunktion ist sichergestellt, dass eine Lösung $\rho_\alpha$ existiert und diese eindeutig ist.

Die Lösung der Gleichung (6) wird mit numerischen Methoden ermittelt.

Ist das zulässige Gesamtrisiko für ein Portfolio vorgegeben, dann wird in der Abbildung 1 der Punkt A für $\alpha = 100\%$ erreicht.

Für $\alpha = 50\%$ ergibt sich als Portfolio dasjenige im Punkt C (Treasury).

Wird die gleiche Verteilung des Vermögens wie in Punkt A angenommen, so ist das Risiko für $\alpha = 50\%$ bestimmt durch die Lage des Punktes B.

Die Wahrscheinlichkeit $\alpha\in [50\%, 100 \%]$ definiert über Gleichung (6) den neuen Schätzer $\rho_\alpha$ für die Korrelation und damit in Abbildung 1 die Lage der Schnittpunkte D und E auf den gestrichelten Verbindungslinien zwischen A, B und C.

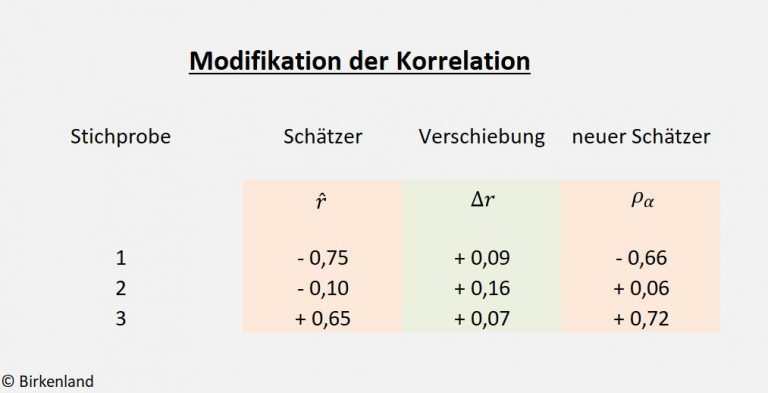
Beispielrechnung

Die folgenden Beispielrechnungen beziehen sich auf drei unterschiedliche Fallstudien jeweils vom Stichprobenumfang $n = 20$ Werte.

Die Beispielrechnung soll die Bestimmung des neuen Schätzers $\rho_\alpha$ mit Hilfe der Gleichung (6) verdeutlichen.

Für die drei Stichproben seien jeweils die Korrelationskoeffizienten $\hat r_1 =-0.75$ , $\hat r_2 = -0.10$ und $\hat r_3 = 0.65$ gemäß Gleichung (3) geschätzt worden.

Die jeweils zugrundeliegende wahre Korrelation $\rho$ sei unbekannt.

Das Konfidenzniveau sei in allen Fällen mit $\alpha = 75 \%$ vorgegeben.

Aus Gleichung (6) berechnen sich schließlich die in der Tabelle 1 angegebenen Werte $\rho_\alpha$ als Schätzer für die unbekannte, wahre Korrelation $\rho$ .

Tabelle 1: Zusammenhang der Schätzer für die Korrelation.

Im Falle einer Gesamtrisikoberechnung für die Stichprobe $(x_i, y_i)$ führt die Verwendung des Korrelationsschätzers $\rho_\alpha$ dazu, dass das Risiko mit einer genau spezifizierten Sicherheit berechnet wird.

Auf der anderen Seite erlaubt dieses Verfahren, dass von einer maximalen Risikoabschätzung (direkte Addition der Einzelrisiken, also Korrelationswert $=+1$ ) systematisch Abstand genommen werden kann.

Das Verfahren liefert folglich bei der Frage der Entscheidung zwischen günstiger und worst case Risikoabschätzung eine statistisch fundierte Kompromisslösung.

Die Abbildung 3 verdeutlichen die Ergebnisse aus Tabelle 1 für die jeweilige Stichprobe.

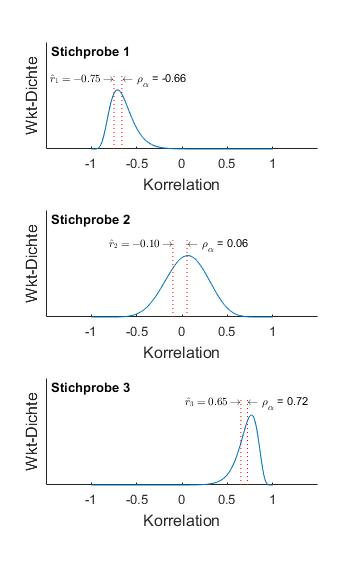
Abbildung 3: Wahrscheinlichkeitsdichten für Stichproben abhängig von der Lage des empirischen Korrelationsschätzers.

Als senkrechte Linien eingezeichnet sind jeweils der empirische Schätzer $\hat r$ und der neue Schätzer $\rho_\alpha$ , vgl. Tabelle 1.

Die Wahrscheinlichkeitsdichte ist zwischen $r \in [-1, +1]$ eingeschränkt und muss daher in der Nähe der Ränder des Intervalls schmaler werden. Dieser Effekt ist umso stärker, je näher sich die empirische Korrelation am Rand des Intervalls befindet. Dies ist in der Abbildung 3 deutlich zu erkennen.

Wie in der Tabelle 1 ist auch in der Abbildung 3 zu erkennen, dass der Wert der Verschiebung $\Delta r = \rho_\alpha - \hat r$ (bei sonst gleichen Parametern) abhängig von der Lage der Wahrscheinlichkeitsdichte im Bereich $[-1, +1]$ ist.

Die obere und unter Grafik zeigt dementsprechend, dass die Verschiebung $\Delta r$ bei schmaler werdender Dichte an den Grenzen kleiner wird. Allgemein gilt, je näher der Schätzwert $\hat r$ bei $\pm 1$ liegt, umso kleiner ist die jeweilige Verschiebung $\Delta r$ .

Der Wert der Korrelation liegt dort mit hoher Wahrscheinlichkeit sehr nahe in der Umgebung von $\hat r$ , so dass nur eine kleine Verschiebung $\Delta r$ erforderlich ist, um dem Sicherheitsbedürfnis $\alpha = 75 \%$ gerecht zu werden.

Literatur

T. Schürmann and I. Hoffmann, On biased correlation estimation, arXiv preprint arXiv:1707.09037, 2017.

H. Markowitz, Journal of Finance, pp. 77, March 1952.

H. Markowitz: Portfolio Selection, 1959.

E.L. Lehmann and G. Casella, Theory of Point Estimation, 2nd. ed., Springer Texts, 1998.

Monatsbericht der Deutschen Bundesbank, Zum aktuellen Stand der bankinternen Risikosteuerung und der Bewertung der Kapitaladäquanz im Rahmen des aufsichtsrechtlichen Überprüfungsprozesses, p. 57, 12/2007.

I. Olkin and J.W. Pratt, Unbiased estimation of certain correlation coefficients, The Annals of Mathematical Statistics, Vol. 29, No. 1, 201-211, 1958.

I.N. Bronstein et. al.: Taschenbuch der Mathematik. 5. Auflage, Verlag Harry Deutsch, p. 801 eq. 16.152b, Frankfurt am Main 2001.

M. Abramowitz and I. Stegun, Handbook of Mathematical Functions, p. 555 eq. 15.1.1., Dover, New York, 1965.

Birkenland

Der Blog für Wissenschaft und Kunst

Modifikation der Korrelation

Definition eines Schätzers für die Korrelation im Rahmen des optimalen Risikomanagements

Einleitung

Korrelationsschätzer und Wahrscheinlichkeitsdichte

Schätzer für die Korrelation gemäß Risikopräferenz

Beispielrechnung

Literatur

Schreibe einen Kommentar Antworten abbrechen

Seiten

Kategorien