Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung

3 Comments
Share

Kritische Werte K_{n,\alpha} für den Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung

Werden die Parameter der Gumbel-Verteilung geschätzt, so können für den Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung nicht die üblichen tabellierten kritischen Werte K_{n, \alpha} genutzt werden.

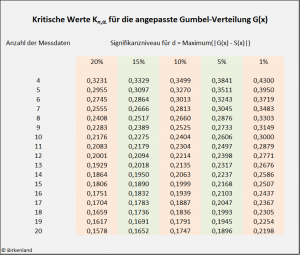
Die nachfolgende Tabelle zeigt die entsprechenden kritischen Werte K_{n, \alpha} für den Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung, wenn die Verteilungsparameter aus vorliegenden Datenpunkten geschätzt worden sind.

Kritische Werte des Kolmogorow-Smirnow-Test für die Gumbel-Verteilung bei geschätzten Verteilungsparametern.

Bei dem Test wird von der Nullhypothese ausgegangen, dass die vorgelegten Daten statistisch durch die Gumbel-Verteilung beschrieben werden.

Ablehnungs- und Annahmebereich für die Nullhypothese werden bei geschätzten Verteilungsparametern durch kritische Werte getrennt, die rund \frac{1}{3} kleiner als die standardmäßig tabellierten Werte sind.

Darüber hinaus sind diese kritischen Werte auch noch abhängig von der zugrundeliegenden Verteilungsfunktion und im Allgemeinen nicht analytisch berechenbar.

Monte-Carlo-Simulationen können dann die benötigten kritischen Werte liefern.

Für den Fall der angepassten Gumbel-Verteilung wurden für den vorliegenden Beitrag Monte-Carlo-Simulationen durchgeführt und die kritischen Werte für den Anpassungstest in obiger Tabelle notiert.

Gütebewertung mit dem Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung

Die Nullhypothese wird zu einem Konfidenzniveau \alpha bei einer Länge der Datenreihe von n Punkten abgelehnt, wenn die Testgröße d des Kolmogorow-Smirnow-Tests größer als der entsprechende kritische Wert K_{n, \alpha} ist.

Konzentration auf kleine Datenbestände

In vielen Anwendungsbereichen können die vorliegenden Datenreihen zur Anpassung der Gumbel-Verteilung sehr kurz und damit eine Gütebewertung unerlässlich sein.

Von besonderem Interesse sind kritische Werte für kleine Datenbestände im Bereich von 4 bis 20 Datenpunkten.

Denn je kleiner der vorgelegte Datenbestand, umso ungenauer kann die Anpassung der Parameter sein und umso wichtiger ist die Überprüfung der Güte der Anpassung.

Daher haben wir uns hier auf diesen Datenumfang konzentriert und die entsprechenden kritischen Werte für den Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung numerisch bestimmt.

Extrapolation auf größere Datenbestände

Sind mehr als n = 20 Datenpunkte in dem vorgelegten Datensatz gegeben, kann der Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung immer noch angewendet werden, wenn die benötigten kritischen Werte simuliert oder aus obiger Tabelle extrapoliert werden.

Eine gute Näherungsformel lässt sich aus folgendem asymptotischen Verhalten der kritischen Werte herleiten:

    \begin{flalign*} \sqrt{m} \, K_{m, \alpha} & = \sqrt{n} \, K_{n, \alpha}.\\ \end{flalign*}

Angenommen für die Datensätze gilt m>n und K_{n, \alpha} sei aus der Tabelle bekannt.

Dann berechnet sich der unbekannte kritische Wert für m Datenpunkte gemäß:

    \begin{flalign*} K_{m, \alpha} & = \sqrt{\frac{n}{m}} \, K_{n, \alpha}.\\ \end{flalign*}

Wir setzen jetzt n = 20.

Somit entsprechen die kritischen Werte zu den verschiedenen Konfidenzniveaus \alpha gerade der letzten Zeile in der obigen Tabelle.

Zur Extrapolation der benötigten kritischen Werte für einen Datensatz von m Datenpunkten gilt dann die Näherungsformel:

    \begin{flalign*} K_{m, \alpha} & = \sqrt{\frac{\text{20}}{m}} \, K_{\text{20}, \alpha}.\\ \end{flalign*}

Dokumentation der Monte-Carlo-Simulation

Es wurden für jede in der Tabelle notierte Anzahl n von Datenpunkten jeweils 500.000 Monte-Carlo-Simulationen durchgeführt.

In jedem einzelnen Monte-Carlo-Simulationsschritt sind n Datenpunkte mit einer Gumbel-Verteilung erzeugt worden. Die Verteilungsparameter waren dabei zwar bekannt, blieben aber für die weiteren Analysen ungenutzt.

Stattdessen wurde jedes Mal eine Anpassung an die n erzeugten Datenpunkten vorgenommen und dabei der Lage- und der Streuungsparameter der Gumbel-Verteilung G(x) berechnet.

Die Anpassung erfolgte mit Hilfe der logarithmierten Maximum-Likelihood-Methode.

Des Weiteren erfolgte eine Berechnung der empirischen Verteilungsfunktion S(x) aus den Datenpunkten.

Das Ergebnis jedes Simulationsschritts war der maximale Abstand d zwischen der angepassten Gumbel-Verteilung G(x) und der empirischen Verteilungsfunktion S(x).

Pro Anzahl n an Datenpunkten sind somit 500.000 maximale Abstandswerte d zufällig erzeugt worden.

Aus der aufsteigend sortierten Reihe der maximalen Abstände d sind zu den entsprechenden Konfidenzniveaus sodann die kritischen Werte für den Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung entnommen worden.

Vergleich mit anderen Ergebnissen

Chandra et al. hat 1981 die kritischen Werte für den Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung im Zusammenhang mit Datenbeständen von zehn und zwanzig Datenpunkte angegeben.

Die von uns simulierten Werte für zehn und zwanzig Datenpunkte entsprechen im Rahmen einer Genauigkeit von \pm 0,001 den von Chandra et al. angegebenen Werten.

3 Comments

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert