Extremwertstatistik im Portfoliomanagement: Latenz operationeller Risiken.
In der gutachterlichen Rückbetrachtung bzgl. der Umsetzung einer Anlagestrategie finden sich mitunter Hinweise darauf, dass manche zur Vermögensverwaltung beauftragte Finanzinstitute auf Jahressicht zwar gute Erfolge vorweisen können, aber unterjährig doch deutliche Verlustrisiken kompensieren mussten, die einen sehr guten Erfolg verhinderten.
Die deutlichen Verlustrisiken zeigen ihre Auswirkung z. B. darin, dass die statistische Bewertung der unterjährigen Wertentwicklung eines Anlageportfolios ein asymmetrisches, tendenziell linksschiefes Verteilungsprofil ausweist.
Oft können erst bei einer nachgelagerten, genaueren Untersuchung der unterjährigen Wertentwicklung des Anlageportfolios die Ursachen für die erhöhten Verluste identifiziert werden.
Nicht wenige Fälle lassen sich dabei im Nachhinein auf Verlustereignisse in Folge schlagend gewordener operationeller Risiken zurückführen.
Diese Risiken wurden bereits 2003 in der Eigenkapitalvorschrift Basel II als die Gefahr von Verlusten angesehen, die durch die Unangemessenheit oder das Versagen von internen Verfahren, Menschen und Systemen oder in Folge externer Ereignisse eintreten.
Es ist zu beobachten, dass bei manchen operationellen Risiken eine gewisse Verzögerung des Erkennens der Wirkung (Latenz) auftritt.
Das ganze Ausmaß macht sich mitunter erst zeitlich versetzt im regelmäßigen Vermögensbericht oder sehr viel später in der umfangreichen, analysierenden Rückschau bemerkbar.
D. h. es besteht die Möglichkeit, dass Verluste, die eigentlich operationellen Risikoereignissen zugeschrieben werden müssten, im Regelbetrieb kurzerhand aber irrtümlich den Marktrisiken zugeordnet werden. Somit bleiben die tatsächlichen Ursachen der Verluste zunächst unentdeckt.
Welche operationellen Risikoereignisse das sein können und wie sie im Vorfeld im Risikomanagement berücksichtigt werden können, ist Kernthema dieses Beitrags.
Demgemäß beschäftigt sich dieser Artikel in erster Linie mit der vorausschauenden Berücksichtigung des Einflusses solcher operationellen Risiken auf die Vermögensentwicklung eines Anlageportfolios.
Darüber hinaus zeigt der Beitrag auch auf, wie die Methoden der Extremwertstatistik im Portfoliomanagement zusätzlich eine Schlechtester-Fall-Abschätzung für den Risikoreport im Rahmen des Risikomanagements erlauben.
Operationelle Risiken
Die in der Finanzbranche eingetretenen und identifizierten Schadensfälle als Folge operationeller Risiken haben insgesamt bereits eine erhöhte Aufmerksamkeit der Finanzinstitute selber, aber auch der Regulatoren (BaFin, EZB etc.) sowie weiterer Gruppen (Kunden- und Geschäftspartner, Öffentlichkeit, Ratingagenturen, Wirtschaftsprüfer, etc.) gegenüber dieser Risikoart bewirkt.
In den letzten Jahren wurden daher verstärkt Anstrengungen unternommen, dieser Risikoart und den damit verbundenen Verlustereignissen mit einem systematischen Controlling und Management als eigenständige Instanz in den Finanzinstituten zu begegnen.
Damit kann ein gewisses Maß an Prävention gegenüber den Verlustrisiken aus fraudulenten Handlungen (interner / externer Betrug) oder den im System des Finanzinstituts zu findenden Gründen (Beschäftigungspraxis, Systemausfälle, Ablauf-, Verfahrens- und Prozessfehler) erreicht werden.
Trotz aller Vorsorge verbleibt aber ein weites Spektrum von Ereignissen, die nahe des Zufälligen zu einem Vermögensschwund führen können.
Die mit diesen Ereignissen verbundenen Verluste werden bisweilen nicht mit operationellen Risiken als Ursache in Verbindung gebracht und daher in der Praxis auch nicht von Verlusten aufgrund von Marktrisiken differenziert.
Selbst wenn später operationelle Risiken als Ursache der Verluste erkannt werden, gelingt es aufgrund der zufälligen Eigenart nur vereinzelt geeignete Maßnahmen zur Begrenzung bzw. Minderung zu ergreifen.
Sogar unter den idealen Bedingungen einer hervorragend funktionierenden Controlling- und Management-Instanz in einem Finanzinstitut können nahezu unentdeckt beispielhaft nachfolgende operationelle Risiken zu Vermögensverlusten führen, die dann u. U. irrtümlich allgemeinen Marktrisiken zugeschrieben werden:
 Art und Struktur:
Art und Struktur:
Es könnten Anlageentscheidungen für Anlageprodukte gefällt werden, obwohl notwendige Vorabanalysen zu Art, Struktur und Wirkung nicht gewissenhaft durchgeführt wurden oder gar Informationen zu den Produkten fehlen, falsch oder nicht plausibel sind (Fahrlässigkeit).
Mit dem Kauf des Anlageproduktes könnte somit durch eine fehlerhafte Risikoklassenzuordnung ungewollt eine Limitüberschreitung in der dem Produkt eigentlich entsprechenden marktbezogenen Risikoklasse verbunden sein.
Werden diese ungedeckten Risiken schlagend, kann es folglich zu unerwarteten Verlusten kommen.
 Prozessmanagement:
Prozessmanagement:
Bei der Zuordnung eines Anlageproduktes zu marktbezogenen Risikokategorien können Kalkulations- oder Eingabefehler zu einer fehlerhaften, unterschätzenden Risikobewertung des Engagements führen.
Die Risikobewertung weist damit für die kommende Beobachtungsperiode eine nicht existierende höhere Sicherheit der Kapitalanlage aus.
Werden die Risiken in der Zwischenzeit schlagend, sind höhere, nicht erwartete Verluste möglich.
Auch kann die Nichtbeachtung einer illiquiden Marktsituation zu einem überteuerten Ankauf von Wertpapieren und damit u. U. zu Liquiditätsengpässen oder erhöhten Zinsaufwendungen führen, die letztendlich als Verluste zu verbuchen sind.
 Portfoliomanagement:
Portfoliomanagement:
In einem guten Marktumfeld können passive Grenzverletzungen auftreten, so dass für einzelne, risikotechnisch korrekt erfasste Produkte die Anlagegrenze nach oben überschritten wird.
Wird die mit der passiven Grenzverletzung zu groß gewordene Anlageposition nicht in angemessener Zeit zügig abgebaut (Fristversäumnis), können beim Einsetzen einer schärferen Marktkorrektur die vormaligen Gewinne nicht verbucht werden und es sind eventuell zu hohe Verluste zu tragen.
Diese aus der Portfoliomanagementpraxis ableitbaren, eher der Fahrlässigkeit zuordenbaren, nicht dolosen operationellen Risiken erzeugen im Eintrittsfall durchweg ein Schadens- und Verlustprofil, das sich den Verlusten aus allgemeinen Marktrisiken überlagert.
Dadurch kann es zu einer linksschiefen Verteilung der unterjährigen Vermögenswertentwicklung kommen, die erst in der statistischen Nachbetrachtung sichtbar wird.
Daher sollte in einer nach vorne gerichteten Risikobetrachtung die Möglichkeit der Latenz operationeller Risiken und deren Einfluss bereits Berücksichtigung finden, vgl. hierzu auch die Mindestanforderungen an das Risikomanagement (MaRisk).
Annahmen der Fallstudie
Für den vorliegenden Beitrag werden einige aus der Praxis entlehnte Annahmen getätigt.
In dieser Fallstudie wird davon ausgegangen, dass im Rahmen des Managements von Vermögenswerten operationelle Risiken ihre Wirkung entfalten, der entstehende Schaden aber – unwissentlich – zunächst den allgemeinen Marktrisiken zugeschrieben wird.
Erst bei einer späteren, umfassenderen Analyse sei eine Differenzierung möglich und Teile der Verluste können Ereigniskategorien der operationellen Risiken zugeschrieben werden.
Weiter wird davon ausgegangen, dass ein institutioneller Anleger das Mandat zum Management seines Vermögens einem Vermögensverwalter eines Finanzinstituts neu erteilt hat.
Somit kann sich die vorausschauende Risikobewertung nicht auf vergangene Entwicklungen des Anlagevermögens stützen.
Der institutionelle Anleger verlangt jedoch im Vorfeld eine Risikobewertung, die auch den Umstand möglicher Verlustereignisse aufgrund operationeller Risiken berücksichtigt und eine Schlechtester-Fall-Abschätzung beinhaltet.
Fragestellungen
- Welche Möglichkeiten gibt es, Verluste bergende operationelle Risiken im Vorfeld in einer Risikoabschätzung zu berücksichtigen?
- Wie kann dann zusätzlich eine Schlechtester-Fall-Abschätzung durchgeführt werden?
Grundidee und Ergebnisvorschau
Die Annahme einer linksschiefen Verteilung ![]() als statistische Modell für die unterjährige Vermögensentwicklung ermöglicht im Vorfeld die Verlustwirkung latenter operationeller Risiken im Portfoliomanagement zu berücksichtigen.
als statistische Modell für die unterjährige Vermögensentwicklung ermöglicht im Vorfeld die Verlustwirkung latenter operationeller Risiken im Portfoliomanagement zu berücksichtigen.
Wie die nachfolgende Grafik zeigt, wird in diesem Beitrag aus dem statistischen Modell ![]() ein weiteres statistisches Modell
ein weiteres statistisches Modell ![]() für den schlechtesten Fall – dem Risiko eines möglichen minimalen Vermögensstands – entwickelt.
für den schlechtesten Fall – dem Risiko eines möglichen minimalen Vermögensstands – entwickelt.
Beide statistischen Modelle zusammen dienen abschließend dazu, die nach vorne gerichtete Risikobewertung hinsichtlich der Fragestellungen durchzuführen.
Vorgehensweise
Zunächst wird eine linksschiefe Verteilungsfunktion als statistisches Modell ![]() für die unterjährige Vermögensentwicklung vorgelegt und deren Verteilungsparameter prognostiziert.
für die unterjährige Vermögensentwicklung vorgelegt und deren Verteilungsparameter prognostiziert.
Diese Verteilungsfunktion dient im ersten Schritt dazu, eine Risikobewertung der künftigen Vermögensentwicklung anhand von Standardrisikokennziffern durchzuführen.
Zur Abschätzung des schlechtesten Falls, wird mit Methoden der Extremwertstatistik vom Modell ![]() aus startend die Verteilung
aus startend die Verteilung ![]() des minimalen Vermögenswertes entwickelt.
des minimalen Vermögenswertes entwickelt.
In diesem Artikel wird beispielhaft die linksschiefe Gumbel-Verteilung als statistisches Modell ![]() für die unterjährige Vermögensentwicklung betrachtet.
für die unterjährige Vermögensentwicklung betrachtet.
Es zeigt sich, dass damit die Verteilung des minimalen Vermögenswertes ebenfalls eine linksschiefe Gumbel-Verteilung ![]() – allerdings mit anderen Verteilungsparametern – ist.
– allerdings mit anderen Verteilungsparametern – ist.
Abschließend wird diese Verteilung genutzt, um die entsprechenden Risikobewertungen und Risikoprognosen des schlechtesten Falls durchzuführen.
Die Vorgehensweise fasst noch einmal die nachfolgende Grafik zusammen:
Einbettung in ein Gesamtkonzept
Im institutionalisierten Rahmen wirken beim Management eines Anlageportfolios die gesetzlichen und aufsichtsrechtlichen Vorgaben u. a. daraufhin, dass das Finanzinstitut jederzeit einen vollständigen und aktuellen Überblick über die Methoden und Verfahren hat, die zur geforderten Risikoquantifizierung im Risikomanagement verwendet werden.
In dem Beitrag Extremwertstatistik im Portfoliomanagement III wurde bereits ausgeführt, dass die Finanzinstitute zur Erfüllung dieser Anforderungen und im Hinblick auf eine prüfungsfeste Darstellung von Selbstkontrollprozessen (Compliance), – wenn möglich – getrennte Instanzen für das Portfoliomanagement und das Risikomanagement installieren sollten.
Wobei eine sorgfältige Abstimmung zwischen Portfoliomanagement und Risikomanagement den allen Rahmenbedingungen und Vorgaben genügenden Anlageerfolg beim Management eines Anlageportfolios garantiert.
Das übergeordnete Gesamtkonzept zur Risikobewertung ist die in den Finanzinstituten durchzuführende Risikoinventur.
Schwerpunkte der Risikoinventur sind die Identifikation wesentlicher Risiken, denen sich ein Institut bei seiner Geschäftstätigkeit ausgesetzt sieht, und die Darstellung möglicher Risikokonzentrationen auf der Basis einer Risikobewertung sämtlicher Geschäftsaktivitäten.
In diesem Rahmen ist auch das Risikomanagement eingeordnet. Dem Risikomanagement fallen hierbei zum überwiegenden Anteil Risikoprüfungs-, Risikomessungs-, Risikobewertungs-, Risikoüberwachungs- und Kontrollaufgaben zu, deren Ergebnisse inkl. Handlungsempfehlungen in einem Risikoreport dokumentiert werden.
Das Risikomanagement von Finanzinstituten umfasst im Ganzen eine Reihe von z. T. interdependenten Risiken.
So sind die Institute neben den finanzwirtschaftlichen Risiken (bspw. Markt- und Kreditrisiken) und leistungswirtschaftlichen Risiken (bspw. Umfeld-, Produkt-, Leistungs- und Beschaffungsrisiken) auch operationellen Risiken ausgesetzt.
Zu letzterer Risikoart gab der Baseler Ausschuss für Bankenaufsicht bereits 2003 eine entsprechende Praxisempfehlung zum Management operationeller Risiken heraus.
Operationelle Risiken finden seither deutlich zunehmend in der Gesetzgebung Beachtung, vgl. z. B. das Amtsblatt der Europäischen Union dort ab Artikel 312.
Im Kern geht es bei dem Management operationeller Risiken um das Erkennen, Bewerten und Überwachen, sowie um das Begrenzen bzw. Mindern der Wirkung entsprechender Risikoereignisse. Ein ausführlicher, regelmäßiger Bericht dokumentiert dabei prüfungsfest die einzelnen Teilaspekte.
Während bedeutende Schadensfälle mit erheblichen Verlusten unverzüglich hinsichtlich ihrer Ursache zu analysieren und meist gut zuordenbar sind, sind bestimmte Schadensfälle oder Beinaheverluste nicht eindeutig zuordenbar und werden u. U. fälschlich mit anderen Risikoereignissen erklärt.
Die novellierte MaRisk setzt hier mit der Vorgabe an, dass die Prozesse zum Management operationeller Risiken auch den Umgang mit nicht eindeutig zuordenbaren Risiken, Beinaheverlusten und zusammenhängenden Ereignissen umfassen sollte.
In dem vorliegenden Beitrag wird ein Weg aufgezeigt, wie eine – ungewollte aber mögliche – Vermengung von Markt- und operationellen Risiken im Portfoliomanagement berücksichtigt werden kann.
Wir konzentrieren uns dabei auf drei Teilaspekte des Risikomanagements, nämlich das Erkennen, Modellieren und Bewerten der Gesamtwirkung in einem Anlageportfolio:
 Es wird zusätzlich von der besonderen Schwierigkeit ausgegangen, dass das Anlageportfolio neu konzipiert wird und somit keine auswertbare Verlustereignisdatenbank vergangener Schadensfälle vorliegt.
Es wird zusätzlich von der besonderen Schwierigkeit ausgegangen, dass das Anlageportfolio neu konzipiert wird und somit keine auswertbare Verlustereignisdatenbank vergangener Schadensfälle vorliegt.
Dadurch wird im Rahmen einer vorausschauenden Bewertung eine Prognose der Gesamtwirkung des Markt- und operationellen Risikos erforderlich.
Diese Prognose kann im laufenden Regelbetrieb anhand der parallel zu pflegenden Ereignisdatenbank plausibilisiert, validiert und wenn nötig entsprechend angepasst werden.
Frühzeitig ist in der Praxis zugleich auch mit der Konzeption und Umsetzung von Maßnahmen zur Begrenzung bzw. Minderung der Gesamtwirkung des Markt- und operationellen Risikos zu beginnen.
Um den Fokus des vorliegenden Beitrags zu wahren, werden diese Teilaspekte hier nicht betrachtet und bleiben anderen Fallstudien vorbehalten.
Beispiel: Stiftungsvermögen
Das Konzept der vorausschauenden Bewertung der Gesamtwirkung von Markt- und operationellem Risiko wird im Folgenden am Beispiel eines Stiftungsvermögens verdeutlicht.
Als institutionellen Anleger betrachten wir eine Stiftung mit einem Stiftungsvermögen von 5 Mrd. Euro.
Die Stiftung habe in unserem Beispiel das Mandat zum Management ihres Anlageportfolios einem Vermögensverwalter erteilt.
Wie schon beschrieben, wollen wir wieder die besonders schwierige Situation annehmen, dass die Stiftung neu gegründet wurde und somit keine Daten über die Portfolioentwicklung in der Vergangenheit vorliegen.
Bekannt ist aber, dass Zustiftungen, Abflüsse und Zinszahlungen, sowie die Bewegungen an den Kapitalmärkten und das aktive Portfoliomanagement des Vermögensverwalters das Stiftungsvermögen künftig beeinflussen werden.
Zur Vereinfachung wird angenommen, dass jeweils zum Wochenstart das Stiftungsvermögen 5 Mrd. Euro beträgt und die beeinflussenden Faktoren im Verlauf der Woche zu einer Vermögensveränderung führen.
Zum Wochenschluss wird der veränderte Vermögensstand notiert und bis zum Start der neuen Woche wird das Vermögen wieder auf 5 Mrd. Euro zurückgeführt.
Der Vermögenswert zum Wochenschluss wird somit mehr oder weniger in der Nähe von 5 Mrd. Euro liegen und von Woche zu Woche um diesen Wert streuen; er unterliegt also einem Zufallsprozess.
Gegenüber unseren bisherigen Beiträgen zum Thema Extremwertstatistik im Portfoliomanagement modifizieren wir das Beispiel etwas und nehmen an, dass die Verteilung der Vermögensstände zum Wochenschluss keiner Normalverteilung, sondern einer linksschiefen Gumbel-Verteilung entspricht.
Wir gehen also von der Prognose aus, dass das mathematische Modell für die Verteilung der wöchentlichen Vermögensendstände eine linksschiefe Gumbel-Verteilung ist (⇒Modellprognose).
Diese Prognose ist z. B. dann gerechtfertigt, wenn es Hinweise darauf gibt, dass es künftig jeweils im Wochenverlauf durch außergewöhnlich negativ wirkende Marktsituationen, durch zusätzliche, unerwartete Entnahmen oder den Auswirkungen von schlagend werdenden operationellen Risiken eher zu deutlichen Unterschreitungen des durchschnittlichen Vermögensstandes von 5 Mrd. Euro kommt.
Viele weitere Modifikationen des Beispiels sind denkbar, doch anhand dieses idealisierten Fallbeispiels wollen wir im Folgenden die Grundidee verdeutlichen, wie bei einer linksschiefen Gumbel-Verteilung eine nach vorne gerichtete Risikobewertung vollständig prognosebasiert erfolgt.
Wir wollen nun, wie im Beitrag Extremwertstatistik im Portfoliomanagement III, der Frage nachgehen, wie für diese Beispiel-Institution ohne Daten die Risikobewertung bezüglich der wöchentlichen Vermögensendstände aber auch hinsichtlich eines minimalen künftigen Vermögensstandes vorgenommen werden kann.
Extremwertstatistik im Portfoliomanagement: Theorie zum Risikomodell
Zunächst wird die linksschiefe Gumbel-Verteilung als mathematisches Modell für die wöchentlichen Vermögensendstände vorgestellt.
Anschließend wird die notwendige Parametertransformation gezeigt, um von diesem mathematischen Modell zu dem Modell für mögliche minimale Vermögensendstände zu gelangen.
Die Gumbel-Verteilung
Allgemein ist die linksschiefe Gumbel-Verteilung ![]() durch folgenden mathematischen Ausdruck gegeben:
durch folgenden mathematischen Ausdruck gegeben:
![]()
Die Funktion ![]() berechnet die Wahrscheinlichkeit, dass die stetige Zufallsgröße
berechnet die Wahrscheinlichkeit, dass die stetige Zufallsgröße ![]() höchstens den Wert
höchstens den Wert ![]() annimmt.
annimmt.
In der vorliegenden Fallstudie des Stiftungsvermögens steht ![]() somit für die zufälligen Vermögensendstände.
somit für die zufälligen Vermögensendstände.
Es gilt also der Zusammenhang: ![]() .
.
Mit ![]() ist der Lageparameter und mit
ist der Lageparameter und mit ![]() der Streuungsparameter der Gumbel-Verteilung bezeichnet.
der Streuungsparameter der Gumbel-Verteilung bezeichnet.
Die Dichte ![]() der Gumbel-Verteilung berechnet sich als Ableitung von
der Gumbel-Verteilung berechnet sich als Ableitung von ![]() zu:
zu:
![]()
Bemerkung: Anschaulich ist mit dem Lageparameter die Lage des Hochpunktes der Dichte beschrieben. Der Lageparameter wird in der Statistik auch als Modalwert bezeichnet. Der Streuungsparameter bemisst – bildhaft ausgedrückt – die Breite des Graphen der Dichtefunktion.
Die Gumbel-Verteilung der wöchentlichen Vermögensendstände
Wir gehen von der Prognose aus, dass die wöchentlichen Vermögensendstände statistisch durch eine linksschiefe Gumbel-Verteilung ![]() mit den Parametern
mit den Parametern ![]() beschrieben werden (⇒Parameterprognose).
beschrieben werden (⇒Parameterprognose).
Aus den Parametern ![]() (Lageparameter) und
(Lageparameter) und ![]() (Streuungsparameter) der hier als linksschief angenommenen Gumbel-Verteilung
(Streuungsparameter) der hier als linksschief angenommenen Gumbel-Verteilung ![]() sollen nun die Parameter der Gumbel-Verteilung
sollen nun die Parameter der Gumbel-Verteilung ![]() der Vermögensminima abgleitet werden.
der Vermögensminima abgleitet werden.
Von der Modellprognose ![]() wird nun also auf das mathematische Modell
wird nun also auf das mathematische Modell ![]() für die Verteilung der Vermögensminima geschlossen.
für die Verteilung der Vermögensminima geschlossen.
Dazu gehen wir von dem in der Literatur beschriebenen mathematischen Beweisergebnis aus, dass die ursprüngliche Gumbel-Verteilung im Anziehungsbereich einer zweiten Gumbel-Verteilung liegt.
D. h. vereinfacht ausgedrückt, die Verteilung der Minima der linksschiefen Gumbel-Verteilung ![]() ist wieder eine linksschiefe Gumbel-Verteilung.
ist wieder eine linksschiefe Gumbel-Verteilung.
Wir bezeichnen diese neue Gumbel-Verteilung mit ![]() und werden im Folgenden deren Parameter bestimmen.
und werden im Folgenden deren Parameter bestimmen.
Die Gumbel-Verteilung der Vermögensminima
Der Übergang von ![]() zu
zu ![]() wird mathematisch im Rahmen der Analyse des Anziehungsbereichs vollzogen.
wird mathematisch im Rahmen der Analyse des Anziehungsbereichs vollzogen.
Diese Analyse führt zu dem Ergebnis, dass die Parameter der beiden linksschiefen Gumbel-Verteilungen über folgende Transformationsformeln zusammenhängen:
![]()
Während der Streuungsparameter ![]() sich nicht verändert, verschiebt sich der Lageparameter
sich nicht verändert, verschiebt sich der Lageparameter ![]() zu kleineren Vermögenswerten hin.
zu kleineren Vermögenswerten hin.
Die Verschiebung des Lageparameters wird umso größer, je größer die anfängliche Streuung ![]() war und je mehr Perioden
war und je mehr Perioden ![]() im Beobachtungszeitraum betrachtet werden.
im Beobachtungszeitraum betrachtet werden.
Plausibilisierung der Transformationsformeln
An dieser Stelle wollen wir keinen strengen Beweis für die obigen Transformationsformeln von ![]() zu
zu ![]() geben, sondern diese mit bereits bekannten Ergebnissen plausibilisieren.
geben, sondern diese mit bereits bekannten Ergebnissen plausibilisieren.
In unserem Beitrag Extremwertstatistik im Portfoliomanagement II hatten wir für die Verteilungsfunktion des Minimums ![]() – für
– für ![]() Wochen im Beobachtungszeitraum – folgende Darstellung hergeleitet:
Wochen im Beobachtungszeitraum – folgende Darstellung hergeleitet:
![]()
In der Gleichung bedeutete ![]() die Dichte der Verteilung der wöchentlichen Vermögensendstände.
die Dichte der Verteilung der wöchentlichen Vermögensendstände.
Im vorliegenden Fall setzen wir somit ![]() .
.
Die Dichte ![]() ist hier also gleich der linksschiefen Gumbel-Dichte
ist hier also gleich der linksschiefen Gumbel-Dichte ![]() .
.
Das Integral über ![]() liefert die Gumbel-Verteilung
liefert die Gumbel-Verteilung ![]() , d. h. wir können etwas vereinfachen und notieren:
, d. h. wir können etwas vereinfachen und notieren:
![]()
Die Analyse des Anziehungsbereichs umfasst im Allgemeinen die Untersuchung der rechten Seite der vorgenannten Gleichung für den Fall, dass ![]() gegen unendliche strebt.
gegen unendliche strebt.
Es wird bei dieser Art der Analyse gezeigt, dass ![]() im Limes
im Limes ![]() einer linksschiefen Gumbel-Verteilung entspricht.
einer linksschiefen Gumbel-Verteilung entspricht.
Auf dem gleichen Weg zeigen wir jetzt, dass die beiden Gumbel-Verteilungen ![]() und
und ![]() über obige Transformationsformeln verknüpft sind.
über obige Transformationsformeln verknüpft sind.
In unserem Fall muss ![]() sich also im Limes
sich also im Limes ![]() aus
aus ![]() berechnen lassen.
berechnen lassen.
Wir überprüfen dieses durch die folgende Rechnung:
![Rendered by QuickLaTeX.com \begin{flalign*} G_1(m_n) & = \lim_{n\rightarrow\infty} G(m_n) \\ & = \lim_{n\rightarrow\infty} \left\{ 1 - \left[ 1 - G_0(m_n) \right]^{n}\right\}\\ & = \lim_{n\rightarrow\infty} \left\{1 - \left[ 1 - 1 + \exp\left(-\exp\left(\frac{m_n-a_0}{b_0}\right)\right)\right]^{n}\right\}\\ & = \lim_{n\rightarrow\infty} \left\{1 - \left[ \exp\left(-\exp\left(\frac{m_n-a_1 - b_1 \ln(n) }{b_1}\right)\right)\right]^{n}\right\}\\ & = \lim_{n\rightarrow\infty} \left\{1 - \left[ \exp\left(-\exp\left(\frac{m_n-a_1}{b_1}\right) \exp\left(-\ln(n)\right)\right)\right]^{n}\right\}\\ & = \lim_{n\rightarrow\infty} \left\{1 - \left[ \exp\left(-\exp\left(\frac{m_n-a_1}{b_1}\right) \frac{1}{n}\right)\right]^{n}\right\} \\ & = 1 - \exp\left(-\exp\left(\frac{m_n-a_1}{b_1}\right) \right). \\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-b8d9e5ed718c36518a2fd3742456423e_l3.png)
In der zweitletzten Gleichung kürzt sich die Potenz von ![]() gerade mit der Potenz
gerade mit der Potenz ![]() , so dass der Term hinter dem Limes unabhängig von der Periodenzahl
, so dass der Term hinter dem Limes unabhängig von der Periodenzahl ![]() wird und die Limesbildung damit entfällt.
wird und die Limesbildung damit entfällt.
Der durch die Transformationsformeln gebildete Zusammenhang zwischen ![]() und
und ![]() gilt also streng für jedes
gilt also streng für jedes ![]() und ist somit keine Näherung.
und ist somit keine Näherung.
Diese Besonderheit wird im Zusammenhang mit minimalen Extremwerten mathematisch als min-stabil bezeichnet.
Anwendung des Risikomodells 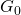
Die Gesamtwirkung des Markt- und operationellen Risikos wird im hier betrachteten Anwendungsfall durch die statistische Verteilung ![]() beschrieben.
beschrieben.
Mit dieser Verteilung können sämtliche Standardrisikomesszahlen bestimmt und in einem Risikoreport ausgewiesen werden.
Beispielhaft seien folgende Standardrisikokennziffern aufgeführt:
Weniger zum Standard gehören die Risikoabschätzungen zum schlechtesten Fall im Rahmen der Extremwertstatistik und sollen daher ausführlicher vorgestellt werden.
Die Möglichkeit über den schlechtesten Fall Aussagen abzuleiten, bietet das statistische Modell ![]() der Vermögensminima.
der Vermögensminima.
Die Anwendung des Modells ![]() bzw.
bzw. ![]() betrachten wir jetzt im Detail.
betrachten wir jetzt im Detail.
Extremwertstatistik im Portfoliomanagement: Anwendung des Risikomodells 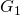
Die Abbildung 1 zeigt mit dem roten Graphen die Anpassung der Gumbel-Dichte ![]() und damit mögliche Ausprägungen minimaler Vermögensstände der Stiftung.
und damit mögliche Ausprägungen minimaler Vermögensstände der Stiftung.

Abbildung 1: Darstellung der prognostizierten Dichte für den Volumenbestand zum Wochenschluss (grün) und die jährlichen Minima (rot).
Die Abbildung zeigt außerdem die prognostizierte Gumbel-Dichte ![]() der Verteilung des Stiftungsvermögens (grün) um den zentralen Wert von 5 Mrd. Euro.
der Verteilung des Stiftungsvermögens (grün) um den zentralen Wert von 5 Mrd. Euro.
Es handelt sich hierbei um eine linksschiefe Gumbel-Verteilung, die den prognostizierten Lageparameter ![]() von 5 Mrd. Euro besitzt.
von 5 Mrd. Euro besitzt.
Beide Gumbel-Dichten sind in der Grafik geeignet skaliert in willkürlichen Einheiten über dem Stiftungsvermögen in Euro aufgetragen.
Ausgehend von dem Stiftungsvermögen von 5 Mrd. Euro wird erwartet, dass am Wochenschluss das Vermögen irgendwo innerhalb einer Bandbreite von etwa 4,93 Mrd. Euro bis 5,04 Mrd. Euro liegt. Dies entspricht in etwa dem Überdeckungsbereich der grün eingezeichneten Dichte.
Der Streuungsparameter ![]() wird in diesem Fall auf rund ein Achtel der Bandbreite prognostiziert und mit 0,014 Mrd. Euro notiert.
wird in diesem Fall auf rund ein Achtel der Bandbreite prognostiziert und mit 0,014 Mrd. Euro notiert.
In diesem Fallbeispiel interessieren wir uns für die Verteilung des Vermögensminimums in den kommenden ![]() 52 Wochen bei wöchentlicher Feststellung des Vermögensendstandes.
52 Wochen bei wöchentlicher Feststellung des Vermögensendstandes.
Mit den oben angegebenen Transformationsformeln wird der Lageparameter der Gumbel-Verteilungsdichte ![]() für die Vermögensminima somit wie folgt berechnet:
für die Vermögensminima somit wie folgt berechnet:
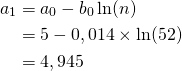
Wir erhalten also für die Dichte ![]() der Gumbel-Verteilung den Lageparameter
der Gumbel-Verteilung den Lageparameter ![]() = 4,945 Mrd. Euro.
= 4,945 Mrd. Euro.
Der Streuungsparameter der Dichte ![]() entspricht gemäß der Transformationsformel dem Streuungsparameter der Verteilung der Vermögensendstände.
entspricht gemäß der Transformationsformel dem Streuungsparameter der Verteilung der Vermögensendstände.
D. h., es ist ![]() 0,014 Mrd. Euro.
0,014 Mrd. Euro.
Für diese Parameter ![]() und
und ![]() überdeckt die Dichte der Gumbel-Verteilung (rot) in der Abbildung 1 einen bestimmten Wertebereich des Stiftungsvermögens und markiert damit (für die Wahl
überdeckt die Dichte der Gumbel-Verteilung (rot) in der Abbildung 1 einen bestimmten Wertebereich des Stiftungsvermögens und markiert damit (für die Wahl ![]() 52) die möglichen Lagen des minimalen Vermögenswertes im nächsten Jahr.
52) die möglichen Lagen des minimalen Vermögenswertes im nächsten Jahr.
Daraus folgt ein weiteres Ergebnis: Wenn im nächsten Jahr ein minimales Stiftungsvermögen auftritt, dann liegt dieses bei wöchentlicher Vermögenswertfeststellung mit hoher Wahrscheinlichkeit irgendwo in der Bandbreite zwischen 4,87 Mrd. Euro und 4,98 Mrd. Euro.
Der Erwartungswert und die Varianz der Gumbel-Verteilung für Minimalwerte können aus den Parametern ![]() und
und ![]() der Dichte bestimmt werden:
der Dichte bestimmt werden:
![Rendered by QuickLaTeX.com \begin{flalign*} \mathrm{E}[m] & = a_1 - b_1\gamma \\ \mathrm{Var}[m] & = \frac{\pi^2 b_1^2}{6}.\\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-883ab8b07916413eb537bf9df0fb3795_l3.png)
Hierbei ist ![]() die Euler-Mascheroni-Konstante.
die Euler-Mascheroni-Konstante.
Der Erwartungswert wird daher gerundet mit 4,937 Mrd. Euro notiert. Die Standardabweichung als Wurzel der Varianz berechnet sich gerundet zu 0,018 Mrd. Euro.
Dieses Ergebnis kann vereinfacht wie folgt interpretiert werden: Wird im kommenden Jahr ein Vermögensminimum registriert, so liegt dieses Minimum mit einer Wahrscheinlichkeit von rund 70 % in dem Bereich zwischen 4,919 Mrd. Euro und 4,955 Mrd. Euro um den Erwartungswert von 4,937 Mrd. Euro.
Nebenrechnung:
4,919 Mrd. Euro = (4,937 – 0,018) Mrd. Euro
4,955 Mrd. Euro = (4,937 + 0,018) Mrd. Euro
Das Integral über die geschätzte Dichte ![]() zwischen Untergrenze (4,919 Mrd. Euro) und Obergrenze (4,955 Mrd. Euro) liefert die Wahrscheinlichkeit von rund 70 %.
zwischen Untergrenze (4,919 Mrd. Euro) und Obergrenze (4,955 Mrd. Euro) liefert die Wahrscheinlichkeit von rund 70 %.
Damit ist für die Stiftung auf Jahressicht die Wahrscheinlichkeit für das Auftreten eines Vermögensminimums in diesem Wertebereich bemessen.
Die Eintrittswahrscheinlichkeit für den Schaden, dass überhaupt ein Vermögensminimum kleiner oder gleich dem Modalwert ![]() auftritt, kann in gleicher Weise durch Integration von
auftritt, kann in gleicher Weise durch Integration von ![]() vom linken Rand – bei minus Unendlich – bis zum Modalwert
vom linken Rand – bei minus Unendlich – bis zum Modalwert ![]() berechnet werden und liegt hier bei unter 2 %.
berechnet werden und liegt hier bei unter 2 %.
Letzteres entspricht dem Wert der Gumbel-Verteilung ![]() an der Stelle des Lageparameters
an der Stelle des Lageparameters ![]() .
.
Extremwertstatistik im Portfoliomanagement: Risikobewertung im Risikoreport
Neben der Darstellung der Standardrisikomesszahlen würden nach der obigen Analyse nun zusätzlich im Risikoreport Aussagen über den schlechtesten Fall möglich sein.
Sowohl bei den Standardrisikomesszahlen als auch bei der Prognose im Hinblick auf den schlechtesten Fall handelt es sich um eine nach vorne gerichtete Betrachtung der Gesamtwirkung des Markt- und operationellen Risikos.
Auf Basis der zuvor abgeleiteten Ergebnisse würde die Risikoprognose zur Vermögensentwicklung die Standardrisikokennziffern und zur schlechtesten Entwicklung des Stiftungsvermögens im kommenden Jahr den Erwartungswert des minimalen Vermögensstands zu Grunde legen.
Wir zeigen speziell zum minimalen Vermögensstand eine mögliche (Kurz-)Darstellung der Ergebnisse im kombinierten Risikoreport / Steuerungsreport.
Risikoreport / Steuerungsreport – Auszug
Im Risikoreport des Risikomanagements für das Stiftungsvermögen könnte – nach der Erläuterung des verwendeten Verfahrens – im einfachsten Fall zum möglichen Vermögensminimum folgende Formulierung stehen:
Die Modellprognose und die Prognose der Modellparameter für die Vermögensbestände zum Wochenschluss führen zu folgender Risikoeinschätzung: Wenn im kommenden Jahr ein minimales Vermögen auftritt, dann dürfte es in der Nähe des Erwartungswertes bei etwa 4,937 Mrd. Euro liegen.
Abhängig vom gewünschten Detailgrad können bei Bedarf alle Analyseergebnisse (Vermögensminimum, Wertebereich der Schwankung, Eintrittswahrscheinlichkeit, etc.) in den Risikoreport als Bestandteil der Risikoprognose integriert werden.
Je nachdem, ob diese Risikoprognose im Einklang mit den Vorgaben z. B. in den Anlagerichtlinien steht oder nicht, muss gegebenenfalls die Zusammensetzung des Portfolios neu gestaltet werden.
Risikoreport / Steuerungsreport – weitere Inhalte
Neben der ausführlichen Kommentierung der Risikoprognose und -bewertung mit den statistischen Modellen (![]() und
und ![]() ) sind entsprechende Handlungsempfehlungen (inkl. Notfallmaßnahmen) für das Portfoliomanagement ebenfalls im Report zu dokumentieren (⇒Einzelrisikobetrachtung).
) sind entsprechende Handlungsempfehlungen (inkl. Notfallmaßnahmen) für das Portfoliomanagement ebenfalls im Report zu dokumentieren (⇒Einzelrisikobetrachtung).
Die Kommentierung beschreibt außerdem das konkret absehbare Risiko aus dem Portfoliomanagement im Zusammenhang mit anderen Risikoarten unter Einbezug des aktuellen Kenntnisstandes über diese weiteren Risikoarten und im Hinblick auf deren zukünftig erwartete Entwicklung (⇒Gesamtrisikobetrachtung).
Folgende Bestandteile sind somit mindestens in der Kommentierung zum Einzel- und Gesamtrisiko aufzunehmen:
- Auswirkungen und mögliche Folgen für den Geschäftsbetrieb.
- Konkrete Beschreibung des Risikos und des Verfahrens der Risikobewertung, differenziert nach Einzel- und Gesamtrisiko.
- Prognose der künftigen Risikoentwicklung, differenziert nach Einzel- und Gesamtrisiko, unter Berücksichtigung der Interdependenz der Risikoarten.
- Wenn schon vorliegend: Bezug zu bereits eingetretenen, protokollierten Verlusten.
- Beschreibung von bereits eingeleiteten oder beabsichtigten Maßnahmen zur Risikominderung.
Speziell bei der Einzelrisikobetrachtung betrifft die Definition und Beschreibung der Maßnahmen dabei nicht ausschließlich die im Portfoliomanagement zu treffenden Vorkehrungen, sondern auch die zu ergreifenden, geschäftspolitischen Gegenmaßnahmen für den Fall, dass operationelle Risiken im Nachgang als Auslöser für Verluste identifiziert werden können.
Extremwertstatistik im Portfoliomanagement: Qualität der Modelltransformation 
Es stellt sich abschließend die Frage, wie gut repräsentiert das Modell ![]() tatsächlich die minimalen Vermögenswerte, wenn das statistische Modell
tatsächlich die minimalen Vermögenswerte, wenn das statistische Modell ![]() als Verteilung der wöchentlichen Vermögensendstände angenommen wird?
als Verteilung der wöchentlichen Vermögensendstände angenommen wird?
In dem hier skizzierten besonderen Fall, dass die Ausgangsverteilung der wöchentlichen Vermögensendstände einer Gumbel-Verteilung entspricht, ist der Zusammenhang zu der Gumbel-Verteilung, die die Vermögensminima beschreibt, exakt.
Der Zusammenhang ist durch die oben notierten Transformationsformeln gegeben.
Zur Validierung vergleichen wir die oben abgeleiteten Ergebnisse mit den Resultaten einer Monte Carlo Simulation.
Wir nutzen also die Möglichkeit, den Funktionsverlauf der Dichte ![]() qualitativ zu bewerten.
qualitativ zu bewerten.
Dazu wird ein optischer Vergleich der Dichte ![]() mit einer durch Monte Carlo Simulation erhaltenen Dichte
mit einer durch Monte Carlo Simulation erhaltenen Dichte ![]() durchgeführt.
durchgeführt.
Im Rahmen der Monte Carlo Simulation wurden 1 Mio. Vermögensminima mit der prognostizierten Verteilung ![]() des Vermögensbestandes erzeugt.
des Vermögensbestandes erzeugt.
Anschließend wurde die Maximum-Likelihood-Methode verwendet, um aus den Vermögensminima die Parameter ![]() und
und ![]() der Gumbel-Verteilungsdichte
der Gumbel-Verteilungsdichte ![]() zu bestimmen.
zu bestimmen.
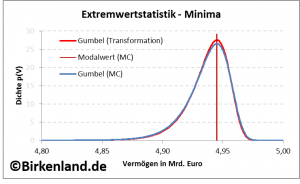
Die folgende Abbildung zeigt den optischen Vergleich der zwei Dichten.
Die Abbildung 2 zeigt als rote Kurve die Gumbel-Dichte ![]() im Vergleich zu der simulierten Dichte
im Vergleich zu der simulierten Dichte ![]() in blau für
in blau für ![]() 52 Wochen.
52 Wochen.
Zusätzlich eingezeichnet ist der Lageparameter ![]() als Modalwert der Gumbel-Dichten (weinrot).
als Modalwert der Gumbel-Dichten (weinrot).
Es ist zu erkennen, dass die zwei Dichten fast exakt übereinander liegen und den gleichen Modalwert besitzen.
Zusätzlich zu diesem optischen Vergleich wurden die simulierten mit den berechneten Parameter (hier: ![]() und
und ![]() mit
mit ![]() und
und ![]() ) verglichen.
) verglichen.
Ergebnis: Die simulierten weichen von den numerisch berechneten Parametern lediglich in der fünften Stelle hinter dem Komma voneinander ab.
Wegen der erkennbar nahezu perfekten Deckung der Dichten untereinander und der numerisch fast gleichen Parameter schlussfolgern wir, dass beide Dichten statistisch das gleiche Phänomen beschreiben.
D. h., die über die Transformationsformeln abgeleitete Gumbel-Dichte ![]() beschreibt statistisch die Vermögensminima.
beschreibt statistisch die Vermögensminima.
Einwertung und Grenzen des Verfahrens
Bei der abschließenden Einwertung des vorgestellten Verfahrens zur Bewertung eines möglichen schlechtesten Falls gelten die gleichen Ausführungen, die wir bereits in unserem Beitrag Extremwertstatistik im Portfoliomanagement III dargelegt haben.
Das hier vorgeschlagene systematische Verfahren zur Risikobewertung gestattet auf der Basis von Prognosen eine erste, indikative Einschätzung des zu erwartenden Risikos mit Blick auf das mögliche Vermögensminimum in einem gewählten künftigen Zeitraum.
Der künftige Zeitraum sollte nicht zu lang gewählt werden und im Idealfall eine kombinierte Wahl von ![]() 12, 24 und 52 Wochen umfassen.
12, 24 und 52 Wochen umfassen.
Im Verlauf der ersten drei Monaten des Portfoliomanagements wird bereits eine kleine Datenbasis aufgebaut, so dass das hier beschriebene Verfahren und die daraus abgeleiteten Risikoprognosen in diesem Anwendungszeitraum stets einer Überprüfung im Rahmen eines Backtestings unterzogen werden können.
Eine Möglichkeit bietet ein fortlaufender Test der Güte der Anpassung mit Hilfe des Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung.
Führt die Validierung zu notwendigen Anpassungen – beispielsweise hinsichtlich der Verteilungsannahme – so sind entsprechenden Anpassungen umgehend durchzuführen und in der Änderungsdokumentation zum Prozess zu protokollieren.
Ebenso ist beim Vorhandensein einer Datenbasis ein Wechsel des Verfahren möglich, so dass dann die Risikobewertung mit dem Verfahren aus unserem Beitrag Extremwertstatistik im Portfoliomanagement II erfolgen kann.
Eine besondere Sorgfalt sollte auch hier bei der Abschätzung des Prognoserisikos walten.
Insbesondere die Verteilungsannahme, dass die linksschiefe Gumbel-Verteilung ![]() die wöchentlichen Vermögensendstände statistisch beschreibt, und die Prognose der entsprechenden Parameter (
die wöchentlichen Vermögensendstände statistisch beschreibt, und die Prognose der entsprechenden Parameter (![]() ,
, ![]() ) unterliegen dem Risiko, dass sie mit einem Fehler behaftet sind. Eine Prüfmöglichkeit bietet hier ebenfalls der Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung.
) unterliegen dem Risiko, dass sie mit einem Fehler behaftet sind. Eine Prüfmöglichkeit bietet hier ebenfalls der Kolmogorow-Smirnow-Test bei der Gumbel-Verteilung.
Aus diesem Prognoserisiko kann dann eine mögliche Fehlbewertung des Risikos erwachsen, die sich folglich in allen Risikokennziffern bemerkbar macht.
Die Größenordnung der Fehlbewertung gilt es in jedem Fall abzuschätzen. Hierzu haben wir im Beitrag Extremwertstatistik im Portfoliomanagement III bereits eine praktikable Lösung vorgeschlagen.
Die Möglichkeit und der abgeschätzte Umfang der Fehlbewertung sollte ebenfalls als Grenze des Verfahrens in einem Fachkonzept dokumentiert werden.
Um abschließend den Einfluss des Prognoserisikos zu mildern, kann das hier vorgestellte Verfahren mit dem von uns entwickelten Konzept der Konservativen Risikobewertung kombiniert werden.
Ganz allgemein können auch hier sämtliche Belange einer Szenarioanalyse und eines aufgeprägten Stresstests berücksichtigt werden.
Das wird möglich, wenn die entsprechenden Vorgaben in dem Risikomodell beispielsweise in den Parametern (![]() ,
, ![]() ) abgebildet werden und die Risikobewertung in jedem Szenario oder Stressfall erneut vorgenommen wird.
) abgebildet werden und die Risikobewertung in jedem Szenario oder Stressfall erneut vorgenommen wird.
Darüber hinaus können sich in der Praxis weitere Grenzen des Verfahrens zeigen. Daher sind alle Ergebnisse im individuellen Einzelfall stets kritisch zu prüfen und anhand weiterer Informationen zu validieren.
Extremwertstatistik im Portfoliomanagement: Literatur
Extremwerttheorie
http://wwwmath.uni-muenster.de/statistik/kabluchko/Skripte/Skript_Extremwerttheorie.pdf
Extremwertstatistik zur Modellbildung
Modelling Extremal Events: for Insurance and Finance
(Embrecht, Klüppelberg, Mikosch im Springer-Verlag, 2001)
Theorie der Extremwertstatistik
https://wwwmath.uni-muenster.de/statistik/loewe/extrem.pdf
Über die Extremwertstatistik und Wiederkehrintervalle in langzeitkorrelierten Systemen
http://www.physik.uni-halle.de/Fachgruppen/kantel/PhD_Eichner.pdf
Ermittlung des Value-at-Risk von Finanzportefeuilles mit Methoden der Extremwertstatistik
http://www.risknet.de/fileadmin/eLibrary/Extremwerttheorie-Diplomarbeit-Frahm.pdf