Extremwertstatistik im Portfoliomanagement: Die Risikobewertung bei einem Datenpunkt.
Anlagerichtlinien geben dem Portfoliomanager das Ziel der Vermögensanlage vor und definieren die Anlagegrenzen. Damit sind die Portfolioausrichtung und der Bewegungsspielraum für den Portfoliomanager festgelegt.
Das Ziel und die Ausrichtung einer Stiftung sind beispielsweise, langfristig Gelder für Förderprojekte einzig aus dem Ertrag ihres Vermögens zur Verfügung zu stellen, also ohne den Kapitalstock – das Stiftungsvermögen – aufzuzehren.
Zusätzlich zu dieser Ertragserwartung fixieren die Anlagerichtlinien aber auch Forderungen an das Risikomanagement.
Initiiert durch rechtliche, aufsichtsrechtliche und/oder satzungsmäßige Vorgaben wird kundenseitig ein regelmäßiger oder anlassbezogener Risikoreport des Risikomanagements erwartet.
Neben den üblichen Risikoparametern Volatilität und Value-at-Risk können auch Prognosen über das zu erwartende Vermögensminimum auf Sicht von einem Jahr eingefordert werden.
Im Fall eines Stiftungsvermögens steckt dahinter die Grundidee, die potenzielle Gefahr eines Aufzehrens des Kapitalstocks abzuschätzen, um nötigenfalls einen Impuls zu generieren, der im Portfoliomanagement ein Gegensteuern auslöst.
In unserem ersten Beitrag zur Extremwertstatistik im Portfoliomanagement haben wir gezeigt, wie eine derartige Risikoprognose aus der Portfolioentwicklung der vergangenen Jahre systematisch abgeleitet werden kann.
Wesentliche Stütze der Risikoprognose im Rahmen der Risikobewertung war die Anpassung einer geeigneten Verteilungsfunktion an die in den vergangenen Jahren aufgetretenen Vermögensminima im Portfolio.
Als eine geeignete Verteilung zur statistischen Beschreibung von minimalen Vermögensständen haben wir die Gumbel-Verteilung identifiziert.
Die Gumbel-Verteilung gab uns u. a. Auskunft darüber, in welcher Größenordnung im kommenden Jahr ein Vermögensminimum erwartet werden kann.
Zur Anpassung der Gumbel-Verteilung an die Vermögensminima der letzten Kalenderjahre wurden die zwei bekanntesten Verfahren genutzt: Die Maximum-Likelihood-Methode und die Momentenmethode.
Beide Methoden erfordern aber mindestens die Vermögensminima der letzten zwei Kalenderjahre, da – vereinfacht ausgedrückt – sonst keine sinnvolle Abschätzung der Breite der Gumbel-Verteilung erfolgen kann.
Problem und Fragestellung
Wir nehmen an, dass lediglich Vermögensbestandsdaten aus dem letzten Kalenderjahr vorliegen.
In den Daten markiert nur ein einziger Vermögensbestand das Vermögensminimum.
Wie kann in diesem Fall eine systematische Risikobewertung für das kommende Kalenderjahr vorgenommen werden?
Welche Möglichkeiten gibt es also, die Methoden der Extremwertstatistik im Portfoliomanagement anzuwenden, wenn nur ein einziger Datenpunkt aus dem letzten Kalenderjahr als Vermögensminimum gegeben ist?
Der vorliegende Beitrag widmet sich genau dieser Fragestellung und zeigt eine Lösungsmöglichkeit auf.
Ziel ist die Entwicklung eines Verfahrens zur systematischen Risikoprognose, das sich von der „naiven“ Prognose – so wie es im letzten Jahr war, wird es im nächsten Jahr auch – abgrenzt und weitere Aussagen zur Risikobewertung ermöglicht.
Zur Verdeutlichung wird durchgängig wieder das Beispiel des Stiftungsvermögens aus dem Beitrag Extremwertstatistik im Portfoliomanagement betrachtet.
Beispiel: Stiftungsvermögen
Als Institution betrachten wir eine Stiftung mit einem Stiftungsvermögen von 5 Mrd. Euro.
Zustiftungen, Abflüsse und Zinszahlungen, sowie die Bewegungen an den Kapitalmärkten beeinflussen das Stiftungsvermögen.
Zur Vereinfachung wird angenommen, dass jeweils zum Wochenstart das Stiftungsvermögen 5 Mrd. Euro beträgt und die beeinflussenden Faktoren im Verlauf der Woche zu einer Vermögensveränderung führen.
Zum Wochenschluss wird der veränderte Vermögensstand notiert und bis zum Start der neuen Woche wird das Vermögen wieder auf 5 Mrd. Euro zurückgeführt.
Viele Modifikationen des Beispiels sind denkbar, doch es reicht dieses vereinfachte, idealisierte Fallbeispiel im Folgenden aus, um die Grundidee der Risikobewertung – ausgehend von einer Datenhistorie von einem Jahr – zu verdeutlichen.
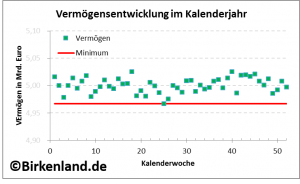
Die nachfolgende Grafik zeigt die engmaschig kontrollierten Vermögensstände der als Beispiel angenommenen Stiftung jeweils zum Wochenschluss im letzten Kalenderjahr.
Als erste Auswertung ist das absolute Minimum des Vermögens im letzten Kalenderjahr als untere Begrenzungslinie (rot) eingezeichnet.
Zu diesem Anwendungsbeispiel hatten wir bereits in dem Beitrag Extremwertstatistik im Portfoliomanagement gezeigt, wie mit Hilfe der Gumbel-Verteilung eine nach vorne gerichtete Risikobewertung des erwarteten minimalen Stiftungsvermögens abgeleitet werden kann.
Die Risikobewertung stützte sich dabei auf die Vermögensminima der letzten zehn Kalenderjahre, die für die Anpassung der Gumbel-Verteilung genutzt werden konnten.
Wir wollen nun der Frage nachgehen, wie für dieses Beispiel die Risikobewertung vorgenommen werden kann, wenn nur Daten des letzten Kalenderjahres vorliegen und damit lediglich ein Vermögensminimum analysiert werden kann?
Grundidee
In einem ersten Schritt wird eine Verteilung ![]() an die Vermögensbestände des letzten Kalenderjahres angepasst.
an die Vermögensbestände des letzten Kalenderjahres angepasst.
D. h. im Fall der Stiftung werden aus den ![]() Wochendaten die Parameter der Verteilung
Wochendaten die Parameter der Verteilung ![]() bestimmt.
bestimmt.
Aus dieser Verteilung der Vermögensbestände kann eine Approximation der gesuchten Verteilung der Vermögensminima hergeleitet werden.
Wir berechnen also aus der Verteilung ![]() eine genäherte Verteilung
eine genäherte Verteilung ![]() für die Vermögensminima.
für die Vermögensminima.
Durch eine geeignete Kurvendiskussion von ![]() erhalten wir Schätzer für die Parameter der gesuchten Verteilung
erhalten wir Schätzer für die Parameter der gesuchten Verteilung ![]() der Vermögensminima.
der Vermögensminima.
Das im letzten Kalenderjahr aufgetretene Vermögensminimum dient abschließend der Bewertung der Güte der Anpassung von ![]() .
.
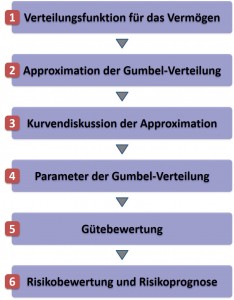
Die folgende Übersicht fast noch einmal die Grundidee zusammen:
Grenzen des Verfahrens
Grundsätzlich ist die Anpassung einer Extremwertverteilung an wenige Datenpunkte eine Herausforderung.
Bei einem Datenpunkt – hier ein Vermögensminimum – ist diese Aufgabe ohne Einbeziehung weiterer Informationen kaum lösbar.
Die Gesamtheit aller Daten – hier alle Vermögensbestände des letzten Kalenderjahres – trägt weitere Informationen.
Wir entwickeln daher ein Verfahren, um aus diesen Daten auf die Parameter der unbekannten Extremwertverteilung zu schließen (Anpassung).
Das ist ein Lösungsweg – neben vielen anderen Möglichkeiten – der sich auf Vorwissen aus der Portfoliotheorie, sowie bestimmte Annahmen und Näherungen stützt.
Eine andere Möglichkeit bietet z. B. die Monte Carlo Simulation, die wir in dem vorliegenden Beitrag jedoch nur zur Absicherung der Ergebnisse verwenden.
Welche Möglichkeit auch genutzt wird, als Endergebnis der Anpassung erhalten wir lediglich Schätzer für die unbekannten Parameter der Extremwertverteilung.
Die Güte der Anpassung kann zwar anhand des einen Vermögensminimums bewertet werden, jedoch sollten in der Praxis weitere Plausibilitätstests, die der jeweiligen individuellen Situation gerecht werden, durchgeführt werden.
Insbesondere auch, weil Aussagen zur Qualität der Schätzer hinsichtlich
- Erwartungstreue
- Konsistenz
- Varianz
im Einzelfall oft nur durch umfangreiche Rechnungen oder Monte Carlo Simulationen zu belegen sind.
Wir halten also fest: Je weniger Daten vorliegen, umso notwendiger ist die Prüfung der Zulässigkeit des Verfahrens im jeweiligen Einzelfall anhand weiterer Informationen.
Extremwertstatistik im Portfoliomanagement: Theorie
In den meisten Anwendungsfällen der Portfoliotheorie wird die Normalverteilung betrachtet.
Für diese Verteilung gilt, dass sie – statistisch gesehen – im Anziehungsbereich der Gumbel-Verteilung liegt.
Einfacher formuliert: Die Normalverteilung besitzt die Gumbel-Verteilung als Verteilung für die Extrema.
Wir konzentrieren uns im Folgenden auf diesen wichtigen Fall, dass die Verteilung ![]() der wöchentlichen Vermögensbestände der Stiftung einer Normalverteilung entspricht.
der wöchentlichen Vermögensbestände der Stiftung einer Normalverteilung entspricht.
Somit können die Extremwerte statistisch durch die Gumbel-Verteilung ![]() beschrieben werden.
beschrieben werden.
Wir nehmen weiter an, dass die Verteilung ![]() der Vermögensbestände bereits vollständig bekannt ist.
der Vermögensbestände bereits vollständig bekannt ist.
D. h. im Vorfeld wurden die Verteilungsparameter ![]() (Erwartungswert bzw. Lageparameter) und
(Erwartungswert bzw. Lageparameter) und ![]() (Streuung) der Verteilung
(Streuung) der Verteilung ![]() bereits bestimmt.
bereits bestimmt.
Approximation 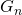 der Extremwertverteilung
der Extremwertverteilung
Die Wahrscheinlichkeit dafür, dass eine Realisierung ![]() der Zufallsvariablen
der Zufallsvariablen ![]() größer als eine vorgegebene Zahl
größer als eine vorgegebene Zahl ![]() ist, lässt sich mit Hilfe der Dichte
ist, lässt sich mit Hilfe der Dichte ![]() der Verteilung
der Verteilung ![]() wie folgt berechnen:
wie folgt berechnen:
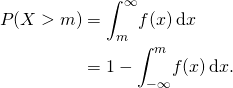
Es wird angenommen, dass alle Realisierungen ![]() der Zufallsvariablen
der Zufallsvariablen ![]() der gleichen Verteilung
der gleichen Verteilung ![]() entstammen.
entstammen.
Bemerkung: Die Werte ![]() stehen hier für die Vermögensbestandsdaten und die Werte
stehen hier für die Vermögensbestandsdaten und die Werte ![]() stehen später für die Vermögensminima. Das Integral in der letzten Zeile entspricht der Verteilung
stehen später für die Vermögensminima. Das Integral in der letzten Zeile entspricht der Verteilung ![]() .
.
Weiter nehmen wir an, dass alle Werte ![]() unabhängig voneinander sind. Wie bei zwei gewürfelten Zahlen in einem Würfelspiel bedeutet dies, dass es zwischen zwei Vermögensbeständen keinen Zusammenhang gibt.
unabhängig voneinander sind. Wie bei zwei gewürfelten Zahlen in einem Würfelspiel bedeutet dies, dass es zwischen zwei Vermögensbeständen keinen Zusammenhang gibt.
Beides mathematisch zusammengefasst besagt, dass die Zufallsvariablen im vorliegenden Fall unabhängig identisch verteilt sind.
Mit diesen Annahmen ist die Wahrscheinlichkeit dafür, dass alle ![]() Realisierungen
Realisierungen ![]() der Zufallsvariablen
der Zufallsvariablen ![]() größer als die vorgegebene Zahl
größer als die vorgegebene Zahl ![]() sind, gegeben durch:
sind, gegeben durch:
![]()
Diese Wahrscheinlichkeit ist gleich der Wahrscheinlichkeit ![]() , dass das Minimum von
, dass das Minimum von ![]() größer als die vorgegebene Zahl
größer als die vorgegebene Zahl ![]() ist.
ist.
Die Gegenwahrscheinlichkeit hierzu lautet:
![]()
Aus dieser Gleichung lässt sich die Approximation ![]() der Verteilung der Minima bestimmen:
der Verteilung der Minima bestimmen:
![]()
Wenn wir diesen Ausdruck nun nach der oberen Integralgrenze ![]() ableiten, erhalten wir einen Ausdruck für die Dichte
ableiten, erhalten wir einen Ausdruck für die Dichte ![]() der Verteilung des Minimums
der Verteilung des Minimums ![]() abhängig von der Dichte
abhängig von der Dichte ![]() der Verteilung der
der Verteilung der ![]() -Werte.
-Werte.
![]()
Dieser letzte Ausdruck ist eine Approximation der gesuchten Dichte ![]() der Gumbel-Verteilung
der Gumbel-Verteilung ![]() für die Minima
für die Minima ![]() und im Allgemeinen abhängig von den Parametern der Dichte
und im Allgemeinen abhängig von den Parametern der Dichte ![]() der Verteilung
der Verteilung ![]() .
.
Aus der Approximation ![]() ermitteln wir nun Schätzer für die Parameter der gesuchten Gumbel-Verteilung
ermitteln wir nun Schätzer für die Parameter der gesuchten Gumbel-Verteilung ![]() .
.
Bemerkung: Die Dichte ![]() ist über der
ist über der ![]() -Achse definiert. Gleiches gilt für die gesuchte Dichte
-Achse definiert. Gleiches gilt für die gesuchte Dichte ![]() der Gumbel-Verteilung
der Gumbel-Verteilung ![]() für Minima. Das Vermögensminimum
für Minima. Das Vermögensminimum ![]() ist lediglich ein spezieller Wert auf der
ist lediglich ein spezieller Wert auf der ![]() -Achse.
-Achse.
Parameterschätzer für die Gumbel-Verteilung
Die Dichte der Gumbel-Verteilung für Minima hat folgende mathematische Darstellung:
![]()
Die Gumbel-Dichte ![]() besitzt zwei – noch unbekannte – Parameter: Den Lageparameter und den Streuungsparameter.
besitzt zwei – noch unbekannte – Parameter: Den Lageparameter und den Streuungsparameter.
In der Dichte ![]() der Gumbel-Verteilung beschreibt
der Gumbel-Verteilung beschreibt ![]() den Lageparameter der Dichte und entspricht anschaulich demjenigen Wert, für den die Dichte ihren Hochpunkt besitzt.
den Lageparameter der Dichte und entspricht anschaulich demjenigen Wert, für den die Dichte ihren Hochpunkt besitzt.
Mathematisch wird dieser Wert auch als der Modalwert bezeichnet.
Verändert sich der Lageparameter ![]() , so verschiebt sich die Dichte entlang der
, so verschiebt sich die Dichte entlang der ![]() -Achse.
-Achse.
Der Parameter ![]() ist ein Streuungsparameter und bestimmt – etwas bildhaft beschrieben – die Breite der Dichte über der
ist ein Streuungsparameter und bestimmt – etwas bildhaft beschrieben – die Breite der Dichte über der ![]() -Achse.
-Achse.
Mit ansteigendem ![]() wird die Dichte flacher und breiter.
wird die Dichte flacher und breiter.
Damit erstrecken sich die möglichen Minima – z. B. die Vermögensminima im Fall der Stiftung – bei größerem ![]() über einen größeren Bereich.
über einen größeren Bereich.
Nachfolgend wollen wir nun Schätzer für die fehlenden Parameter ![]() und
und ![]() der Gumbel-Verteilung für Minima bestimmen.
der Gumbel-Verteilung für Minima bestimmen.
Bemerkung: Da die wahren Parameter ![]() und
und ![]() der Gumbel-Verteilung unbekannt sind und hier geschätzt werden, müssten die Schätzer zur Unterscheidung von den wahren Parametern mit einem ‚Dach‘ gekennzeichnet werden.
der Gumbel-Verteilung unbekannt sind und hier geschätzt werden, müssten die Schätzer zur Unterscheidung von den wahren Parametern mit einem ‚Dach‘ gekennzeichnet werden.
Also z. B. ![]() als Schätzer für den Lageparameter
als Schätzer für den Lageparameter ![]() .
.
Damit die Formeln einfach bleiben und weil keine Verwechselung auftreten kann, wird hier auf diese Notation verzichtet.
Bestimmung des Lageparameters  :
:
Einen Schätzer für den Lageparameter ![]() erhalten wir, wenn wir für die Funktion
erhalten wir, wenn wir für die Funktion ![]() eine Kurvendiskussion durchführen und das Maximum der Funktion
eine Kurvendiskussion durchführen und das Maximum der Funktion ![]() berechnen.
berechnen.
Es wird angenommen, dass der Wert ![]() , für den die Funktion
, für den die Funktion ![]() einen Hochpunkt zeigt, in etwa dem Lageparameter
einen Hochpunkt zeigt, in etwa dem Lageparameter ![]() der Dichte
der Dichte ![]() der Gumbel-Verteilung entspricht.
der Gumbel-Verteilung entspricht.
Wir sind also an demjenigen Wert ![]() interessiert, der den Hochpunkt der Dichte
interessiert, der den Hochpunkt der Dichte ![]() markiert.
markiert.
Das entspricht der Suche nach dem Maximum von ![]() , das wie üblich über die erste Ableitung der Dichte
, das wie üblich über die erste Ableitung der Dichte ![]() bestimmt werden kann.
bestimmt werden kann.
Wenn wir den obigen Ausdruck ![]() nun nach
nun nach ![]() ableiten, berechnet sich folgender Zusammenhang:
ableiten, berechnet sich folgender Zusammenhang:
![Rendered by QuickLaTeX.com \begin{flalign*} \frac{\mathrm{d}g_n(m)}{\mathrm{d} m} = - n (n-1)\, f^2(m) \, &\left[ 1 - \int_{-\infty}^{m} \! f(x) \, \mathrm{d}x \right]^{n-2} \\ + n\, \frac{\mathrm{d}f(m)}{\mathrm{d} m}\, &\left[ 1 - \int_{-\infty}^{m} \! f(x) \, \mathrm{d}x \right]^{n-1}.\\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-c1d582326e7ac1d7252acd60e6ea60cf_l3.png)
Mit der Forderung:
![]()
gelangen wir nach Umstellung der Gleichung und anschließendem Sortieren zu dem Ergebnis:
![]()
Wie schon oben angemerkt, besteht zwischen der Dichte ![]() und der Verteilung
und der Verteilung ![]() der Zusammenhang:
der Zusammenhang:
![]()
Ferner kürzen wir zur Vereinfachung ![]() mit
mit ![]() ab.
ab.
Aus dem obigen Ergebnis lässt sich sodann das Endergebnis kompakter formulieren:
![]()
Da in dieser Gleichung sowohl ![]() als auch
als auch ![]() von
von ![]() abhängig sind, kann mit ihr der Modalwert
abhängig sind, kann mit ihr der Modalwert ![]() berechnet werden, der die Dichte
berechnet werden, der die Dichte ![]() maximiert.
maximiert.
Im Allgemeinen lässt sich diese Gleichung nicht explizit nach ![]() auflösen, so dass numerische Verfahren angewendet werden müssen, um das
auflösen, so dass numerische Verfahren angewendet werden müssen, um das ![]() zu berechnen.
zu berechnen.
Der Modalwert ![]() von
von ![]() ist für uns der Schätzer für den Lageparameter
ist für uns der Schätzer für den Lageparameter ![]() der gesuchten Gumbel-Verteilung:
der gesuchten Gumbel-Verteilung:
![]()
Hinreichendes Kriterium für einen Hochpunkt
Wir unterstellen für praktische Anwendungsfälle, dass die Verteilung ![]() des Vermögensminimums stetig und beliebig oft stetig differenzierbar ist.
des Vermögensminimums stetig und beliebig oft stetig differenzierbar ist.
Vereinfacht ausgedrückt: Die Verteilung ![]() hat keine Sprünge, Kanten und Ecken.
hat keine Sprünge, Kanten und Ecken.
Die erste Ableitung von ![]() (also die zweite Ableitung von
(also die zweite Ableitung von ![]() ) ist dann stetig.
) ist dann stetig.
Eine weitere Analyse zeigt, dass die erste Ableitung bei ![]() ihr Vorzeichen von plus zu minus wechselt.
ihr Vorzeichen von plus zu minus wechselt.
Das Vorzeichenwechselkriterium zeigt damit an, dass bei ![]() tatsächlich ein Maximum der Dichte
tatsächlich ein Maximum der Dichte ![]() vorliegt.
vorliegt.
Bestimmung des Streuungsparameters 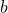 :
:
Einen Schätzer für den Streuungsparameter ![]() erhalten wir, wenn wir die Kurvendiskussion für die Funktion
erhalten wir, wenn wir die Kurvendiskussion für die Funktion ![]() fortsetzen und die Wendepunkte der Funktion
fortsetzen und die Wendepunkte der Funktion ![]() berechnen.
berechnen.
Es wird angenommen, dass der Abstand der Wendepunkte der Funktion ![]() in etwa dem Streuungsparameter
in etwa dem Streuungsparameter ![]() der Dichte
der Dichte ![]() der Gumbel-Verteilung entspricht.
der Gumbel-Verteilung entspricht.
Wir sind also an denjenigen Werten ![]() und
und ![]() interessiert, die die Wendepunkte der Dichte
interessiert, die die Wendepunkte der Dichte ![]() markieren.
markieren.
Wie üblich können die Wendepunkte über die zweite Ableitung der Dichte ![]() bestimmt werden.
bestimmt werden.
Im Folgenden wird der Ausdruck ![]() nun zweimal nach
nun zweimal nach ![]() abgeleitet.
abgeleitet.
Bei Berücksichtigung der obigen Abkürzungen berechnet sich der Zusammenhang:
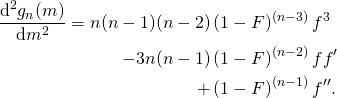
Mit der Forderung:
![]()
kann nach Umstellung der Gleichung und anschließendem Sortieren das kompakte Ergebnis notiert werden:
![]()
Diese Gleichung ist die Bestimmungsgleichung für die Wendepunkte der Funktion ![]() Der Ausdruck
Der Ausdruck ![]() bezeichnet die zweite Ableitung der Dichte
bezeichnet die zweite Ableitung der Dichte ![]() .
.
Da in dieser Gleichung ![]() und
und ![]() wieder von
wieder von ![]() abhängig sind, können mit dieser Gleichung Lösungen
abhängig sind, können mit dieser Gleichung Lösungen ![]() für
für ![]() berechnet werden. Einige dieser Lösungen können zu Wendepunkten der Dichte
berechnet werden. Einige dieser Lösungen können zu Wendepunkten der Dichte ![]() gehören.
gehören.
Im Allgemeinen lässt sich auch diese Gleichung nicht explizit nach ![]() auflösen, so dass numerische Verfahren angewendet werden müssen, um die Wendepunkte der Dichte
auflösen, so dass numerische Verfahren angewendet werden müssen, um die Wendepunkte der Dichte ![]() zu berechnen.
zu berechnen.
Wenn wir davon ausgehen, dass die Gumbel-Verteilung die Verteilung der Minima darstellt, dann sind genau zwei Wendepunkte ![]() und
und ![]() für die Dichte
für die Dichte ![]() zu erwarten.
zu erwarten.
Liegen die Wendepunkte vor, so ist die Hälfte der absoluten Differenz zwischen den Wendepunkten für uns der Schätzer für den Streuungsparameter ![]() der gesuchten Gumbel-Verteilung:
der gesuchten Gumbel-Verteilung:
![]()
Hinreichendes Kriterium für einen Wendepunkt
Es ist im Einzelfall zu prüfen, ob an den Wendepunkten das Vorzeichen der zweiten Ableitung von ![]() wechselt, vgl. das Vorzeichenwechselkriterium.
wechselt, vgl. das Vorzeichenwechselkriterium.
Zusammenfassung der Ergebnisse
Ausgehend von einer Verteilungsfunktion ![]() für den Vermögensbestand wird eine Approximation
für den Vermögensbestand wird eine Approximation ![]() der Extremwertverteilung bestimmt.
der Extremwertverteilung bestimmt.
Eine Analyse der zugehörigen Dichte ![]() liefert spezielle Werte
liefert spezielle Werte ![]() die Schätzungen für die unbekannten Parameter
die Schätzungen für die unbekannten Parameter ![]() und
und ![]() der Dichte der Gumbel-Verteilung
der Dichte der Gumbel-Verteilung ![]() für Minima ermöglichen.
für Minima ermöglichen.
Bestimmungsgleichung für den Modalwert 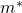 von
von 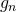
![]()
Die Lösung dieser Gleichung ist der Modalwert ![]() .
.
Der Modalwert führt zu einer Schätzung für den Lageparameter ![]() :
:
![]()
Bestimmungsgleichung für die Wendepunkte 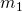 und
und 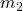 von
von 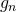
![]()
Die Lösungen dieser Gleichung sind die Wendepunkte ![]() und
und ![]() .
.
Sie führen zu einer Schätzung für den Streuungsparameter ![]() :
:
![]()
Dichte der Gumbel-Verteilung für Minima
Die Dichte ![]() der Gumbel-Verteilung für Minima ist gegeben durch folgenden Ausdruck:
der Gumbel-Verteilung für Minima ist gegeben durch folgenden Ausdruck:
![]()
Die Variable ![]() steht für die Minima.
steht für die Minima.
Der integrierten Dichte entsprechend hat die Gumbel-Verteilung ![]() folgende Gestalt:
folgende Gestalt:
![]()
In den Darstellungen für Dichte und Verteilung setzen wir die zuvor geschätzten Werte für den Lageparameter ![]() und den Streuungsparameter
und den Streuungsparameter ![]() ein.
ein.
Damit sind weitere statistische Untersuchungen der Vermögensminima im Fall der Stiftung möglich.
Eine Analyse der Verteilung ![]() führt z. B. zur Risikobewertung und Risikoprognose, die in einem Risikoreport dokumentiert werden kann.
führt z. B. zur Risikobewertung und Risikoprognose, die in einem Risikoreport dokumentiert werden kann.
Spezialisierung auf die Normalverteilung
Bislang sind die speziellen Eigenschaften der Normalverteilung noch nicht genutzt worden.
Die einzige Annahme über die Verteilungsfunktion ![]() war, dass sie im Anziehungsbereich der Gumbel-Verteilung liegt.
war, dass sie im Anziehungsbereich der Gumbel-Verteilung liegt.
Das Verfahren kann daher in angepasster Form auch auf andere Verteilungsfunktionen ![]() übertragen werden, die diese gleiche Eigenschaft besitzen.
übertragen werden, die diese gleiche Eigenschaft besitzen.
Im Einzelfall ist jedoch die Zulässigkeit der Anwendung des Verfahrens zu prüfen.
Unter Berücksichtigung der Darstellung der Dichte der Normalverteilung werden nun die modifizierten Bestimmungsgleichungen für den Lageparameter ![]() und den Streuungsparameter
und den Streuungsparameter ![]() der Gumbel-Verteilung hergeleitet.
der Gumbel-Verteilung hergeleitet.
Die Darstellung der Dichte der Normalverteilung lautet:
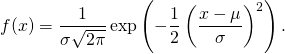
Bei der ersten Ableitung nach ![]() reproduziert sich die
reproduziert sich die ![]() -Funktion, so dass sich für die erste Ableitung ein einfacher Zusammenhang berechnet:
-Funktion, so dass sich für die erste Ableitung ein einfacher Zusammenhang berechnet:
![]()
Ein ähnlich einfacher Zusammenhang berechnet sich für die zweite Ableitung:
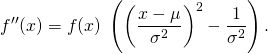
Die Verteilung ![]() hatten wir oben bereits als nicht weiter zu vereinfachendes Integral von
hatten wir oben bereits als nicht weiter zu vereinfachendes Integral von ![]() identifiziert.
identifiziert.
Wir setzten später zur Vereinfachung der Formeln
![]()
Modalwert- und Wendepunktgleichung
Das Einsetzen der vorgenannten Ausdrücke in die Bestimmungsgleichung für den Modalwert liefert den Zusammenhang:
![]()
Werden die obigen Ausdrücke in die Bestimmungsgleichung für die Wendepunkte eingesetzt, so berechnet sich folgende modifizierte Gleichung für die Wendepunkte:
![]()
Diese beiden Bestimmungsgleichungen sind speziell und gelten nur für die Normalverteilung.
Die Dichte ![]() und die Verteilungsfunktion
und die Verteilungsfunktion ![]() sind auch in den modifizierten Bestimmungsgleichungen jeweils für
sind auch in den modifizierten Bestimmungsgleichungen jeweils für ![]() auszuwerten.
auszuwerten.
Weitere Näherung
Die Bestimmungsgleichungen können noch weiter durch die Näherung ![]() vereinfacht werden.
vereinfacht werden.
Diese Näherung ist dann gerechtfertigt, wenn ein Minimum ![]() betrachtet wird, für das
betrachtet wird, für das ![]() sehr kleine Werte annimmt.
sehr kleine Werte annimmt.
Die weitere Näherung kann Vorteile bei der Suche der Nullstellen der Bestimmungsgleichungen haben, ihre Zulässigkeit ist aber im Einzelfall zu prüfen.
Extremwertstatistik im Portfoliomanagement: Anwendung
Die folgende Grafik zeigt mit dem roten Graphen die Anpassung der Gumbel-Dichte ![]() . Der orange Punkt verdeutlicht die Lage des Vermögensminimums im letzten Kalenderjahr.
. Der orange Punkt verdeutlicht die Lage des Vermögensminimums im letzten Kalenderjahr.
Aufgetragen ist die Gumbel-Dichte (in willkürlichen Einheiten) über dem Stiftungsvermögen in Euro.
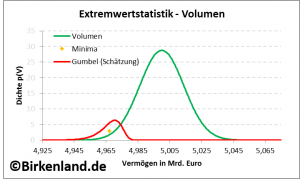
Abbildung 2: Darstellung der Dichte für den Volumenbestand zum Wochenschluss (grün) und die jährlichen Minima (rot). Der orangene Punkt zeigt die Lage des Minimums im letzten Jahr.
Die Abbildung 2 zeigt außerdem die Dichte der Verteilung des Stiftungsvermögens (grün) um den zentralen Wert von 5 Mrd. Euro.
Es handelt sich hierbei um eine Normalverteilung, die den zentralen Wert von 5 Mrd. Euro als Lageparameter ![]() besitzt.
besitzt.
Ausgehend von dem Stiftungsvermögen von 5 Mrd. Euro kann am Wochenschluss das Vermögen gemäß der grün eingezeichneten Dichte irgendwo innerhalb einer Bandbreite von etwa 4,94 Mrd. Euro bis 5,06 Mrd. Euro liegen.
Der Streuungsparameter ![]() ist rund ein Achtel kleiner als diese Bandbreite und hat den exakten Wert von 0,014 Mrd. Euro.
ist rund ein Achtel kleiner als diese Bandbreite und hat den exakten Wert von 0,014 Mrd. Euro.
Die Dichte der Gumbel-Verteilung (rot) überdeckt in der Abbildung 2 einen bestimmten Wertebereich des Stiftungsvermögens und markiert damit die möglichen Lagen des minimalen Vermögenswertes im nächsten Kalenderjahr.
Daraus folgt das erste Ergebnis: Wenn im nächsten Kalenderjahr ein minimales Stiftungsvermögen auftritt, dann liegt dieses mit hoher Wahrscheinlichkeit irgendwo in der Bandbreite zwischen 4,94 Mrd. Euro und 4,98 Mrd. Euro.
Mit den zuvor abgeleiteten Bestimmungsgleichungen wurde der Lageparameter der Gumbel-Verteilung anhand des Modalwerts auf den Wert ![]() 4,971 Mrd. Euro geschätzt.
4,971 Mrd. Euro geschätzt.
Für den Streuungsparameter der Gumbel-Verteilung ergab die Schätzung über die Wendepunkte den gerundeten Wert ![]() 0,006 Mrd. Euro.
0,006 Mrd. Euro.
Der Erwartungswert und die Varianz der Gumbel-Verteilung für Minimalwerte können aus den Parametern ![]() und
und ![]() der Dichte bestimmt werden:
der Dichte bestimmt werden:
![Rendered by QuickLaTeX.com \begin{flalign*} \mathrm{E}[m] & = a - b\gamma \\ \mathrm{Var}[m] & = \frac{\pi^2 b^2}{6}.\\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-85b79b308cc7893a671b2645895dff5e_l3.png)
Hierbei ist ![]() die Euler-Mascheroni-Konstante.
die Euler-Mascheroni-Konstante.
Der Erwartungswert wird daher gerundet mit 4,968 Mrd. Euro notiert. Die Standardabweichung als Wurzel der Varianz berechnet sich gerundet zu 0,007 Mrd. Euro.
Dieses Ergebnis kann vereinfacht wie folgt interpretiert werden: Wird im kommenden Kalenderjahr ein Vermögensminimum registriert, so liegt dieses Minimum mit einer Wahrscheinlichkeit von rund 70 % in dem Bereich zwischen 4,961 Mrd. Euro und 4,975 Mrd. Euro um den Erwartungswert von 4,968 Mrd. Euro.
Nebenrechnung:
4,961 Mrd. Euro = (4,968 – 0,007) Mrd. Euro
4,975 Mrd. Euro = (4,968 + 0,007) Mrd. Euro
Das Integral über die geschätzte Dichte ![]() zwischen Unter- (4,961 Mrd. Euro) und Obergrenze (4,975 Mrd. Euro) liefert die Wahrscheinlichkeit von rund 70 %.
zwischen Unter- (4,961 Mrd. Euro) und Obergrenze (4,975 Mrd. Euro) liefert die Wahrscheinlichkeit von rund 70 %.
Damit ist auf Jahressicht die Wahrscheinlichkeit für das Auftreten eines Vermögensminimums in diesem Wertebereich bemessen.
Vergleiche hierzu auch die Endergebnisse aus dem Beitrag Extremwertstatistik im Portfoliomanagement.
Extremwertstatistik im Portfoliomanagement: Risikobewertung im Risikoreport
Auf Basis der zuvor abgeleiteten Ergebnisse würde die Risikoprognose zur Entwicklung des Stiftungsvermögens im kommenden Kalenderjahr den Erwartungswert zu Grunde legen.
Im Risikoreport des Portfoliomanagers für das Stiftungsvermögen könnte im einfachsten Fall somit folgende Formulierung stehen:
Die statistische Analyse der Vermögensbestände im vergangenen Jahr führt zu folgender Prognose: Wenn im kommenden Jahr ein minimales Vermögen auftritt, dann dürfte es in der Nähe des Erwartungswertes bei etwa 4,968 Mrd. Euro liegen.
Abhängig vom gewünschten Detailgrad können bei Bedarf alle Analyseergebnisse (Vermögensminimum, Wertebereich der Schwankung, Wahrscheinlichkeit, etc.) in den Risikoreport als Bestandteil der Risikoprognose integriert werden.
Je nachdem, ob diese Risikoprognose im Einklang mit den Vorgaben in den Anlagerichtlinien steht oder nicht, muss gegebenenfalls die Zusammensetzung des Portfolios neu gestaltet werden.
Extremwertstatistik im Portfoliomanagement: Güte der Ergebnisse
Es stellt sich abschließend die Frage, wie gut sind diese Ergebnisse?
Bei größeren Datenbeständen stehen mehrere Möglichkeiten zur Verfügung, um die Güte der Anpassung zu bewerten.
Die möglichen Gütetests lassen sich in zwei Gruppen einteilen.
Zum einen sind dies die quantitativen Anpassungstests, die eher auf einer formalen Vorgehensweise beruhen.
Davon zu unterscheiden sind die qualitativen Anpassungstests, die überwiegend auf optische, vergleichende Bewertungsmaßstäbe setzen.
Quantitative Anpassungstests
Die quantitativen Anpassungstests (Hypothesentests) bewerten – vereinfacht dargestellt – den Abstand der empirischen Verteilung von der geschätzten Verteilung.
Beispiele für quantitative Anpassungstests (Auswahl):
- Chi-Quadrat-Test
- Cramér-von-Mises-Test
- Anderson-Darling-Test
- Kullback-Leibler-Divergenz
- Akaike-Informationskriterium
- Kolmogorow-Smirnow-Test
Allen Tests gemeinsam ist, dass sie einen Abstand der Verteilungen als Prüfgröße definieren und gegen einen (tabellierten) kritischen Abstandswert testen.
Als Grundannahme (Hypothese) wird davon ausgegangen, dass die geschätzte Verteilung die empirischen Daten statistisch beschreibt.
Ist die Prüfgröße größer als der kritische Wert, so wird die Hypothese verworfen.
Bei einem einzigen Datenpunkt sind die kritischen Abstandswerte der Statistiken jedoch sehr groß.
Damit wird die Hypothese erst bei sehr deutlichen Abweichungen der Verteilungen verworfen.
So berechnet sich hier für das Beispiel der Stiftung der Kolmogorow-Smirnow-Abstand als Prüfgröße zu ![]() 0,6 und liegt damit bereits für alle üblicherweise tabellierten Konfidenzniveaus deutlich unterhalb des jeweiligen kritischen Wertes für einen Datenpunkt.
0,6 und liegt damit bereits für alle üblicherweise tabellierten Konfidenzniveaus deutlich unterhalb des jeweiligen kritischen Wertes für einen Datenpunkt.
D. h., die Hypothese, dass das eine Vermögensminimum statistisch durch die Gumbel-Verteilung mit obigen Charakteristika beschrieben werden kann, kann nicht für Konfidenzniveaus kleiner als 20 % verworfen werden.
Die Hypothese wird also nur bei sehr deutlichen Abständen der Verteilungen verworfen.
Das ist grundsätzlich kein Problem, wenn das Vermögensminimum tatsächlich statistisch durch die geschätzte Verteilung beschrieben wird.
Wenn aber das Vermögensminimum nicht durch die geschätzte Verteilung (Hypothese) beschrieben wird, sondern durch eine alternative Verteilung (alternative Hypothese), dann zeigt sich, dass die Sensitivität der Tests bei einem Datenpunkt im Allgemeinen gering ist, um die (richtige!) Entscheidung gegen die Hypothese und somit für die alternative Hypothese zu treffen.
Die Aussagekraft der quantitativen Tests ist somit bei einem Datenpunkt nicht sehr ausgeprägt.
Qualitative Anpassungstests
Ebenso wenig aussagekräftig sind die sogenannten PP und QQ Plots.
Hierbei geht es im Kern um einen optischen Vergleich der Lage der Gesamtheit von verschiedenen Punkten (berechnet z. B. aus mehreren Minima) gegenüber einer Geraden in speziellen Grafiken, siehe hierzu auch Extremwertstatistik im Portfoliomanagement.
Bei einem einzigen Vermögensminimum als Datenpunkt ist dieser Vergleich jedoch nur bedingt zielführend.
Es besteht aber die Möglichkeit, den Funktionsverlauf der geschätzten Dichte ![]() qualitativ zu bewerten.
qualitativ zu bewerten.
Dazu wird ein optischer Vergleich der geschätzten Dichte ![]() gegenüber der approximierten Dichte
gegenüber der approximierten Dichte ![]() und einer durch Monte Carlo Simulation erhaltenen Dichte
und einer durch Monte Carlo Simulation erhaltenen Dichte ![]() durchgeführt.
durchgeführt.
Im Rahmen der Monte Carlo Simulation wurden 10.000 Vermögensminima mit der bekannten Verteilung ![]() des Vermögensbestandes erzeugt.
des Vermögensbestandes erzeugt.
Anschließend wurde die Maximum-Likelihood-Methode verwendet, um aus den Vermögensminima die Parameter ![]() und
und ![]() der Gumbel-Verteilung
der Gumbel-Verteilung ![]() zu bestimmen.
zu bestimmen.
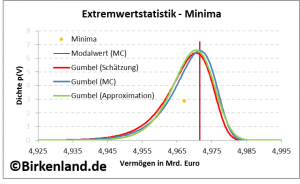
Die folgende Abbildung zeigt den optischen Vergleich der drei Dichten.
Die Abbildung 3 zeigt als rote Linie die mit unserem Verfahren geschätzte Gumbel-Dichte ![]() im Vergleich zu der Approximation
im Vergleich zu der Approximation ![]() (grün) für
(grün) für ![]() 52 Vermögensbestände.
52 Vermögensbestände.
Zusätzlich eingezeichnet ist die simulierte Dichte ![]() in blau, sowie der simulierte Modalwert (weinrot).
in blau, sowie der simulierte Modalwert (weinrot).
Des Weiteren ist das im letzten Kalenderjahr aufgetretene Vermögensminimum als orangener Punkt eingetragen.
Es ist zu erkennen, dass alle drei Dichten sehr eng übereinander liegen und nahezu den gleichen Modalwert besitzen.
Da außerdem der Modalwert nahe dem tatsächlich gemessenen Vermögensminimum liegt, können wir insgesamt aus dem optischen Vergleich schlussfolgern, dass die Vermögensminima gut durch unsere geschätzte Dichte ![]() der Gumbel-Verteilung für Minima statistisch beschrieben werden.
der Gumbel-Verteilung für Minima statistisch beschrieben werden.
Extremwertstatistik im Portfoliomanagement: Literatur
Extremwerttheorie
http://www.math.uni-muenster.de/statistik/kabluchko/Skripte/Skript_Extremwerttheorie.pdf
Extremwertstatistik zur Modellbildung
Modelling Extremal Events: for Insurance and Finance
(Embrecht, Klüppelberg, Mikosch im Springer-Verlag, 2001)
Theorie der Extremwertstatistik
https://wwwmath.uni-muenster.de/statistik/loewe/extrem.pdf
Über die Extremwertstatistik und Wiederkehrintervalle in langzeitkorrelierten Systemen
http://www.physik.uni-halle.de/Fachgruppen/kantel/PhD_Eichner.pdf
Ermittlung des Value-at-Risk von Finanzportefeuilles mit Methoden der Extremwertstatistik
http://www.risknet.de/fileadmin/eLibrary/Extremwerttheorie-Diplomarbeit-Frahm.pdf
Extremwertstatistik im Portfoliomanagement IV - Birkenland
[…] dem Beitrag Extremwertstatistik im Portfoliomanagement III wurde bereits ausgeführt, dass die Finanzinstitute zur Erfüllung dieser Anforderungen und […]