Extremwertstatistik im Portfoliomanagement: Die Risikobewertung ohne Daten.
Dieser Beitrag beschäftigt sich im Kern mit der Lösung zur Frage, wie kann ohne Rückgriff auf Daten vergangener Entwicklungen eine angemessene Risikobewertung bei einem neu konzipierten Anlageportfolio durchgeführt werden?
Anlagerichtlinien geben dem Portfoliomanager das Ziel der neu zu gestaltenden Vermögensanlage vor und definieren die Anlagegrenzen. Damit sind die Portfolioausrichtung und der Bewegungsspielraum für den Portfoliomanager bei der künftigen Kapitalanlage festgelegt.
Das Ziel und die Ausrichtung einer Stiftung sind beispielsweise, langfristig Gelder für Förderprojekte einzig aus dem Ertrag ihres Vermögens zur Verfügung zu stellen, also ohne den Kapitalstock – das Stiftungsvermögen – aufzuzehren.
Zusätzlich zu dieser Ertragserwartung fixieren die Anlagerichtlinien aber auch Forderungen an das Risikomanagement.
Neben den üblichen Risikoparametern Volatilität und Value-at-Risk können als ein Bestandteil der Risikobewertung auch Prognosen über das zu erwartende Vermögensminimum auf Sicht von beispielsweise einem Jahr eingefordert werden.
Im Fall eines Stiftungsvermögens steckt dahinter die Grundidee, die potenzielle Gefahr eines teilweisen oder gänzlichen Aufzehrens des Kapitalstocks abzuschätzen, um nötigenfalls einen Impuls zu generieren, der im Portfoliomanagement ein Gegensteuern auslöst.
Portfoliomanagement und Risikomanagement: Einbettung in ein Gesamtkonzept
Wir betrachten jetzt den Fall, dass ein institutioneller Anleger – beispielsweise die vorgenannte Stiftung – einen Vermögensverwalter beauftragt, sein Vermögen unter Beachtung der Anlagerichtlinien gewinnbringend am Kapitalmarkt anzulegen.
Der beauftragte Vermögensverwalter erbringt dabei als Manager des Anlagevermögens eine Finanzdienstleistung und unterliegt gesetzlichen und aufsichtsrechtlichen Regelungen.
Im institutionalisierten Rahmen wirken beim Management eines Anlageportfolios die gesetzlichen und aufsichtsrechtlichen Vorgaben u. a. daraufhin, dass das Vermögensverwaltungsinstitut (im Folgenden kurz: Institut) jederzeit einen vollständigen und aktuellen Überblick über die Methoden und Verfahren hat, die zur geforderten Risikoquantifizierung im Risikomanagement verwendet werden.
Zur Erfüllung dieser Anforderungen und im Hinblick auf eine prüfungsfeste Darstellung von Selbstkontrollprozessen (Compliance) wird das anlegende Institut angehalten sein, getrennte Instanzen für das Portfoliomanagement und das Risikomanagement zu installieren.
Beim Management eines Anlageportfolios garantiert eine sorgfältige Abstimmung zwischen Portfoliomanagement und Risikomanagement den allen Rahmenbedingungen und Vorgaben genügenden Anlageerfolg.
Portfoliomanagement und Risikomanagement können als Bestandteil eines fortwährenden Regelkreises mit eng verzahnten Kommunikationsbeziehungen betrachtet werden.
Durch die enge Verbindung beider Instanzen, wird oft auch verkürzend und subsumierend von dem Portfoliomanagement gesprochen, gemeint sind dann aber beide Managementaufgaben.
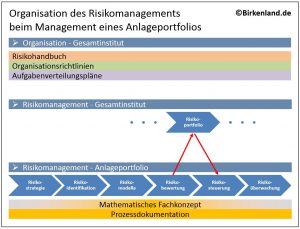
Dem Risikomanagement fallen hierbei zum überwiegenden Anteil Risikoprüfungs-, Risikomessungs-, Risikobewertungs-, Risikoüberwachungs- und Kontrollaufgaben zu, deren Ergebnisse in einem Risikoreport dokumentiert werden.
Die Einbettung des speziell mit dem Anlageportfolio verbundenen Risikomanagements in das entsprechende auf Gesamtinstitutsebene wirkende Konzept zeigt folgendes Schaubild:
Die Rückwirkungen der Ergebnisse auf das Portfoliomanagement und die Handlungsempfehlungen des Risikomanagements werden üblicherweise im Rahmen des den Risikoreport ergänzenden Steuerungsreports dargestellt.
Der Steuerungsreport enthält wesentliche Hinweise für das Portfoliomanagement zur Risikosteuerung.
Die Risikosteuerung soll dabei durch aktive Beeinflussung darauf abzielen, das Risiko zu mindern, bzw. die Eintrittswahrscheinlichkeit einer ermittelten Risikoposition zu verringern oder eine Begrenzung der Risikoauswirkung herbeizuführen.
Risiko- und Steuerungsreport können in der Praxis in einem Dokument zusammengefasst werden und sind unter Beachtung gesetzlicher Vorgaben regelmäßig und anlassbezogen als Bestandteil einer umfassenderen Risikoinventur und zur Information des beauftragenden institutionellen Anlegers zu erstellen.
Schwerpunkte der Risikoinventur sind die Identifikation wesentlicher Risiken, denen sich ein Institut bei seiner Geschäftstätigkeit ausgesetzt sieht, und die Darstellung möglicher Risikokonzentrationen auf der Basis einer Risikobewertung sämtlicher Geschäftsaktivitäten.
In diesem Beitrag beschäftigen wir uns speziell mit der Bewertung von Marktrisiken – genauer mit der Identifikation von Risikospitzen – in einem Anlageportfolio als einen Beitrag zur Risikoinventur (Risikokategorie: Finanzwirtschaftliche Risiken).
Bezogen auf das Anlageportfolio können daraus entsprechende Risiko mitigierende Maßnahmen abgeleitet werden.
So kann beispielsweise die Gegenüberstellung und Einwertung der Ergebnisse der Risikobewertung gegen
- ein vorhandenes Risikodeckungspotential,
- eine zuvor identifizierte Risikotragfähigkeit oder
- eine vorgegebene Risikoübernahmebereitschaft
Basis zur Ableitung von Handlungsempfehlungen / Steuerungsimpulsen für das Portfoliomanagement und damit ein möglicher Auslöser von Änderungen der Portfoliozusammensetzung sein.
Die Zielrichtung der Handlungsempfehlungen des Risikomanagements für das Portfoliomanagement steht unter der Maßgabe, Marktrisiken nicht schlagend werden zu lassen. D. h. ein als zu hoch identifiziertes Marktrisiko und dessen mögliche künftige Realisierung zu vermeiden.
Dementsprechend sind die Anforderungen an die zur Risikobewertung eingesetzten Verfahren, die zugehörigen Fachkonzepte, die Daten-, Parametrisierungs-, Prozess-, Anwendungs- und Ergebnisdokumentationen hoch.
Der Fokus der in diesem Beitrag behandelten Risikobewertung liegt auf der Bemessung eines möglichen, künftigen minimalen Vermögensbestands und behandelt damit, wie schon erwähnt, lediglich einen Teilaspekt der deutlich weiter greifenden Risikoinventur.
Zur Einbettung in ein übergeordnetes Risikoportfolio auf Gesamtinstitutsebene werden wir den Schaden sowohl in seiner Höhe (Euro), als auch bezüglich seiner Eintrittswahrscheinlichkeit (Prozent) quantifizieren.
Wirkungszusammenhänge und Korrelationseffekte zu anderen Risikoarten sind darüber hinaus im individuellen Anwendungsfall auf Gesamtinstitutsebene im Rahmen der Risikoidentifikation / Risikomodellierung darzustellen und zu bewerten.
Dieser Prozessschritt wird in diesem Beitrag nicht betrachtet.
Als ein wesentliches Risiko für das anlegende Institut sei im Zusammenhang mit dem Anlageportfolio ein künftiger minimaler Vermögensbestand identifiziert worden, der bestimmte Schwellwerte unterschreitet.
Die adäquate Modellierung und Bewertung dieses Risikos ist das zentrale Thema dieses Beitrags.
Die folgende Ausarbeitung zum Verfahren der Abschätzung eines künftigen minimalen Vermögensbestands in der Risikobewertung ist so gestaltet, dass sie individuell angepasst in ein entsprechendes Fachkonzept überführt werden kann, welches die verwendeten Methoden und Modelle inklusive der zu berücksichtigenden Anwendungsgrenzen transparent, konsistent und für externe Kontrollinstanzen nachprüfbar beschreibt.
Wir behandeln dabei den schwierigen Spezialfall, dass bei einer Neugestaltung des Anlageportfolios keine Daten vorliegen und die Erstindikation bei der Risikobewertung sich vollständig auf Prognosen gründen muss.
In unserem ersten Beitrag zur Extremwertstatistik im Portfoliomanagement hatten wir gezeigt, wie eine Risikoprognose aus der Portfolioentwicklung der vergangenen Jahre systematisch abgeleitet werden kann.
Wesentliche Stütze der Risikoprognose im Rahmen der Risikobewertung war dort die Anpassung einer geeigneten Verteilungsfunktion an die in den vergangenen Jahren aufgetretenen Vermögensminima im Portfolio.
Als eine geeignete Verteilung zur statistischen Beschreibung von minimalen Vermögensständen hatten wir die Gumbel-Verteilung identifiziert.
Die Gumbel-Verteilung gab uns u. a. Auskunft darüber, in welcher Größenordnung beispielsweise im kommenden Jahr ein Vermögensminimum erwartet werden kann.
Zur Anpassung der Gumbel-Verteilung an die Vermögensminima der letzten Kalenderjahre wurden die zwei bekanntesten Verfahren genutzt: Die Maximum-Likelihood-Methode und die Momentenmethode, vergleiche zur Maximum-Likelihood-Methode auch unseren Beitrag Parameterschätzung bei der Gumbel-Verteilung.
Beide Methoden erfordern aber mindestens die Vermögensminima der letzten zwei Kalenderjahre, da – vereinfacht ausgedrückt – sonst keine sinnvolle Abschätzung der Breite der Gumbel-Verteilung erfolgen kann.
Wenn keine Daten vorliegen, ist die Anwendung dieser beiden Methoden nicht möglich.
Im Folgenden werden wir daher den Ansatz aus dem Beitrag Extremwertstatistik im Portfoliomanagement konsequent weiter entwickeln, um zu einem Verfahren zu gelangen, dass auf der Basis von Prognosen in der Startphase eines neugestalteten Anlageportfolios eine Indikation des minimalen Vermögensbestandes im Rahmen einer Risikobewertung erlaubt.
Problem und Fragestellung
Wir nehmen an, dass keine Vermögensbestandsdaten vergangener Entwicklungen des Portfolios vorliegen. Dies entspricht u. a. dem Fall, dass das Vermögen in einem Anlageportfolio mit neuer strategischer Ausrichtung investiert worden ist.
Es besteht also keine Möglichkeit ein statistisches Modell an vergangene Vermögensminima anzupassen, um damit eine Vorhersage über künftige Vermögensminima im Rahmen der Risikobewertung durchzuführen.
Daraus erwächst die Frage, wie unter solchen Bedingungen trotzdem eine systematische Risikobewertung vorgenommen werden kann?
Welche Möglichkeiten gibt es also, die Methoden der Extremwertstatistik im Portfoliomanagement anzuwenden, wenn keine Daten aus den letzten Kalenderjahren als Vermögensminima gegeben sind?
Der vorliegende Beitrag widmet sich genau dieser Fragestellung und zeigt eine Lösungsmöglichkeit auf.
Inhalt dieser Ausarbeitung ist dabei die konkrete Entwicklung eines Verfahrens zur systematischen Risikoprognose, das auch weitere Aussagen zur Risikobewertung ermöglicht.
Zur Verdeutlichung wird durchgängig wieder das Beispiel des Stiftungsvermögens aus dem Beitrag Extremwertstatistik im Portfoliomanagement betrachtet.
Beispiel: Stiftungsvermögen
Als institutionellen Anleger betrachten wir eine Stiftung mit einem Stiftungsvermögen von 5 Mrd. Euro.
Die Stiftung habe in unserem Beispiel das Mandat zum Management ihres Anlageportfolios einem Vermögensverwalter erteilt.
Wie schon beschrieben, wollen wir hier die besonders schwierige Situation annehmen, dass die Stiftung neu gegründet wurde und somit keine Daten über die Portfolioentwicklung in der Vergangenheit vorliegen.
Bekannt ist aber, dass Zustiftungen, Abflüsse und Zinszahlungen, sowie die Bewegungen an den Kapitalmärkten und das aktive Portfoliomanagement des Vermögensverwalters das Stiftungsvermögen künftig beeinflussen werden.
Zur Vereinfachung wird angenommen, dass jeweils zum Wochenstart das Stiftungsvermögen 5 Mrd. Euro beträgt und die beeinflussenden Faktoren im Verlauf der Woche zu einer Vermögensveränderung führen.
Zum Wochenschluss wird der veränderte Vermögensstand notiert und bis zum Start der neuen Woche wird das Vermögen wieder auf 5 Mrd. Euro zurückgeführt.
Der Vermögenswert zum Wochenschluss wird somit mehr oder weniger in der Nähe von 5 Mrd. Euro liegen und von Woche zu Woche um diesen Wert streuen; er unterliegt also einem Zufallsprozess.
Viele Modifikationen des Beispiels sind denkbar, doch es reicht dieses vereinfachte, idealisierte Fallbeispiel im Folgenden aus, um die Grundidee der Risikobewertung für den Fall zu verdeutlichen, dass keine Daten vorliegen und die Risikobewertung vollständig prognosebasiert erfolgt.
Zu diesem Anwendungsbeispiel hatten wir bereits in dem Beitrag Extremwertstatistik im Portfoliomanagement gezeigt, wie mit Hilfe der Gumbel-Verteilung eine nach vorne gerichtete Risikobewertung auf Basis des erwarteten minimalen Stiftungsvermögens abgeleitet werden kann.
Die Risikobewertung stützte sich dabei auf die Vermögensminima der letzten zehn Kalenderjahre, die für die Anpassung der Gumbel-Verteilung genutzt werden konnten.
Wir wollen nun der Frage nachgehen, wie für diese Beispiel-Institution ohne Daten die Risikobewertung hinsichtlich eines minimalen künftigen Vermögensbestandes vorgenommen werden kann.
Grundidee und Ergebnisvorschau
Als Ergebnis unserer Überlegungen wird ein vollständig prognosebasiertes Verfahren vorgestellt, mit dem eine geeignete Risikobewertung auf der Basis zu erwartender Vermögensminima möglich ist.
In einem ersten Schritt wird dazu eine Verteilung ![]() der zum Wochenschluss zu verzeichnenden Vermögensbestände angenommen. D. h., wir führen eine Modellprognose für die Verteilung der Wochenschlussstände des Vermögens durch.
der zum Wochenschluss zu verzeichnenden Vermögensbestände angenommen. D. h., wir führen eine Modellprognose für die Verteilung der Wochenschlussstände des Vermögens durch.
In den meisten Anwendungsfällen der Portfoliotheorie wird als Verteilung ![]() die Normalverteilung betrachtet.
die Normalverteilung betrachtet.
Wir konzentrieren uns daher hier zunächst auf den wichtigen Fall, dass die Verteilung der wöchentlichen Vermögensbestände der Stiftung einer Normalverteilung entspricht.
Für das Stiftungsvermögen wird also prognostiziert, dass die Normalverteilung das mathematische Modell für die Verteilung der Vermögensbestände zum Wochenschluss ist.
Es wird weiter angenommen, dass Prognosen der Verteilungsparameter ![]() (Erwartungswert bzw. Lageparameter) und
(Erwartungswert bzw. Lageparameter) und ![]() (Streuung) der Normalverteilung
(Streuung) der Normalverteilung ![]() vorliegen.
vorliegen.
Die Normalverteilung liegt – statistisch gesehen – im Anziehungsbereich der die Extrema mathematisch beschreibenden Gumbel-Verteilung.
Einfacher formulierte: Die Normalverteilung besitzt die Gumbel-Verteilung als Verteilung ihrer Extrema.
In dem Beitrag Extremwertstatistik im Portfoliomanagement II hatten wir Methoden erarbeitet, mit deren Hilfe die Parameter der Gumbel-Verteilung ![]() der Vermögensminima aus der Normalverteilung
der Vermögensminima aus der Normalverteilung ![]() berechnet werden können.
berechnet werden können.
Diese Methoden soll im Folgenden genutzt und auf den Fall, das keine Daten zur Verfügung stehen, angepasst werden.
Die Verteilung ![]() dient abschließend dann dazu, die Risikobewertung durchzuführen.
dient abschließend dann dazu, die Risikobewertung durchzuführen.
Die folgende Übersicht fast noch einmal die Grundidee grafisch zusammen:
Im Kern wird also aus der Normalverteilungsannahme und der Prognose der Parameter der Normalverteilung eine Prognose der Verteilungsparameter der Gumbel-Verteilung ![]() der Vermögensminima (Risikomodell) abgeleitet und die Risikobewertung vorgenommen.
der Vermögensminima (Risikomodell) abgeleitet und die Risikobewertung vorgenommen.
Grenzen des Verfahrens
Grundsätzlich ist die Anpassung einer Extremwertverteilung an wenige Datenpunkte eine Herausforderung.
Wenn keine Daten vorliegen, ist diese Aufgabe nur auf der Basis geeigneter Annahmen und Prognosen zu lösen.
Ausgehend von Prognosen über das Verteilungsmodell und die Verteilungsparameter für die wöchentlichen Vermögensbestände, werden Parameter der Gumbel-Verteilung der Vermögensminima abgeleitet.
Bei dieser Vorgehensweise überträgt sich die Prognoseunsicherheit hinsichtlich des Verteilungsmodells und der Verteilungsparameter (zusammengefasst als Modellrisiko) direkt auf die Risikobewertung.
Um den Einfluss dieses Meta-Risikos abzuschätzen und zu mildern sind laufende Plausibilisierungen, Validierungen, Überprüfungen und Verfahrensanpassungen – ggf. durch Experten, die die Modelle nicht entwickelt haben – im jeweiligen konkreten Anwendungsfall angezeigt.
In der Praxis ist auch bei dem hier vorgestellten Verfahren zur Risikobewertung somit viel Erfahrung und Expertenwissen erforderlich, um die Ergebnisse anhand weiterer Informationen (beispielsweise ein Peer-Gruppen-Vergleich ähnlicher Portfolios) zu validieren und das Modellrisiko zu reduzieren.
Vor diesem Hintergrund kann die nachfolgend dargestellte Vorgehensweise lediglich ein erster Schritt im Sinne einer Indikation für das zu erwartende Risiko sein.
Das vorgeschlagene Verfahren bietet einen Lösungsweg – neben vielen anderen Möglichkeiten – der sich auf Vorwissen aus der Portfoliotheorie, sowie bestimmte Annahmen und Näherungen stützt.
Vor dem Hintergrund der getätigten Annahmen und Näherungen ist die Stabilität und Konsistenz der Methode, sowie die Aussagekraft der damit ermittelten Risiken durch die fachlich zuständigen Experten im Einzelfall kritisch zu analysieren.
Eine Möglichkeit der Validierung bietet z. B. die Monte Carlo Simulation, die wir in dem Beitrag Extremwertstatistik im Portfoliomanagement II zur Absicherung der dortigen Ergebnisse bereits vorgestellt und verwendet hatten.
Die Monte Carlo Simulation dient auch in der vorliegenden Fallstudie zur Überprüfung unserer Ergebnisse.
Sie ist außerdem eine Möglichkeit, um die Risikobewertung unabhängig von dem hier vorgeschlagenen Lösungsweg durchzuführen.
Welche Möglichkeit auch genutzt wird, als Endergebnis der Anpassung des statistischen Modells erhalten wir lediglich Schätzer für die unbekannten Parameter der Extremwertverteilung, mit der die für den Risikoreport benötigten Risikogrößen berechnet werden können.
Die Güte der Anpassung kann mit den gängigen Verfahren aufgrund fehlender Daten nicht bewertet werden. In der Praxis ist daher die Durchführung weiterer Plausibilitätstests, die der jeweiligen individuellen Situation gerecht werden, ebenso dringend angeraten, wie deren ausreichende und prüfungsfeste Dokumentation.
Insbesondere auch, weil Aussagen zur Qualität der Schätzer hinsichtlich
- Erwartungstreue
- Konsistenz
- Varianz
im Einzelfall – wenn überhaupt möglich – oft nur durch umfangreiche Rechnungen oder Monte Carlo Simulationen zu belegen sind.
Allgemein kann festgehalten werden: Je weniger Daten vorliegen, umso notwendiger ist die Prüfung der Zulässigkeit des Verfahrens im jeweiligen Einzelfall anhand weiterer Informationen.
Denn Prognosefehler – hinsichtlich des Modells und/oder der Modellparameter – führen unweigerlich zu Fehlern in der Risikobewertung.
Die angemessene und kritische Plausibilisierung der Ergebnisse gilt ganz besonders, wenn sie vollständig prognosebasiert abgeleitet worden sind und – wie im vorliegenden Fall – nicht anhand von Daten überprüft werden können.
Extremwertstatistik im Portfoliomanagement: Theorie zum Risikomodell
Aus den Parametern ![]() (Erwartungswert bzw. Lageparameter) und
(Erwartungswert bzw. Lageparameter) und ![]() (Streuung) der Normalverteilung
(Streuung) der Normalverteilung ![]() sollen nun die Parameter der Gumbel-Verteilung
sollen nun die Parameter der Gumbel-Verteilung ![]() der Vermögensminima abgleitet werden.
der Vermögensminima abgleitet werden.
Die Normalverteilung
Die Darstellung der Dichte der Normalverteilung lautet:
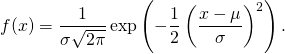
Die Variable ![]() steht für die möglichen Vermögensbestände des Portfolios.
steht für die möglichen Vermögensbestände des Portfolios.
Es bezeichnen ![]() den prognostizierten Erwartungswert bzw. Lageparameter und
den prognostizierten Erwartungswert bzw. Lageparameter und ![]() die prognostizierte Streuung.
die prognostizierte Streuung.
Wir setzen später zur Vereinfachung der Formeln:
![]()
Die Verteilungsfunktion ![]() der Normalverteilung berechnet sich durch folgende Integration aus der Dichte
der Normalverteilung berechnet sich durch folgende Integration aus der Dichte ![]() :
:
![]()
Mit ![]() ist hier die Integrationsvariable bezeichnet.
ist hier die Integrationsvariable bezeichnet.
Die Gumbel-Verteilung
Die Gumbel-Verteilung ![]() ist durch folgenden mathematischen Ausdruck gegeben:
ist durch folgenden mathematischen Ausdruck gegeben:
![]()
Die Variable ![]() steht für die Minima.
steht für die Minima.
Mit ![]() ist der noch unbekannte Lageparameter und mit
ist der noch unbekannte Lageparameter und mit ![]() der noch unbekannte Streuungsparameter der Gumbel-Verteilung bezeichnet.
der noch unbekannte Streuungsparameter der Gumbel-Verteilung bezeichnet.
Die Dichte ![]() der Gumbel-Verteilung für Minima berechnet sich als Ableitung von
der Gumbel-Verteilung für Minima berechnet sich als Ableitung von ![]() zu:
zu:
![]()
Modalwert- und Wendepunktgleichung
In dem Beitrag Extremwertstatistik im Portfoliomanagement II hatten wir Bestimmungsgleichungen für den Modalwert ![]() , sowie die Wendepunkte
, sowie die Wendepunkte ![]() und
und ![]() einer Approximation
einer Approximation ![]() von
von ![]() hergeleitet.
hergeleitet.
Aus dem Modalwert und den Wendepunkten konnten wir die gesuchten Parameter der Gumbel-Verteilung ![]() der Vermögensminima berechnen.
der Vermögensminima berechnen.
Für den Fall, dass ![]() die Normalverteilung und
die Normalverteilung und ![]() die Dichte der Normalverteilung ist, hatten die Bestimmungsgleichungen folgende Gestalt:
die Dichte der Normalverteilung ist, hatten die Bestimmungsgleichungen folgende Gestalt:
Modalwertgleichung
![]()
Wendepunktgleichung
![]()
Der diskrete Zeitparameter ![]() gibt an, über wie viele künftige Zeitperioden das Vermögensminimum betrachtet werden soll.
gibt an, über wie viele künftige Zeitperioden das Vermögensminimum betrachtet werden soll.
Beschreibt die Verteilung ![]() beispielsweise die Entwicklung der Vermögensbestände auf Wochensicht (= Zeitperiode), so kann mit der Wahl
beispielsweise die Entwicklung der Vermögensbestände auf Wochensicht (= Zeitperiode), so kann mit der Wahl ![]() 52 eine statistische Aussage über das Vermögensminimum in den kommenden 52 Wochen – also auf Jahressicht – getroffen werden.
52 eine statistische Aussage über das Vermögensminimum in den kommenden 52 Wochen – also auf Jahressicht – getroffen werden.
Die Dichte ![]() und die Verteilungsfunktion
und die Verteilungsfunktion ![]() sind in den Bestimmungsgleichungen jeweils für
sind in den Bestimmungsgleichungen jeweils für ![]() auszuwerten.
auszuwerten.
In beiden Gleichungen bedeutet somit
![]()
Parameter der Gumbel-Verteilung
Die Lösung der Modalwertgleichung lieferte in unserem Beitrag Extremwertstatistik im Portfoliomanagement II den Modalwert ![]() von
von ![]() .
.
Der Modalwert führte zu einer Schätzung des Lageparameters ![]() von
von ![]() :
:
![]()
Die Lösungen der Wendepunktgleichung sind die Wendepunkte ![]() und
und ![]() von
von ![]() .
.
Sie führten zu einer Schätzung des Streuungsparameters ![]() von
von ![]() :
:
![]()
Bemerkung 1: Da die wahren Parameter ![]() und
und ![]() der Gumbel-Verteilung unbekannt sind und hier geschätzt werden, müssten die Schätzer zur Unterscheidung von den wahren Parametern mit einem ‚Dach‘ gekennzeichnet werden.
der Gumbel-Verteilung unbekannt sind und hier geschätzt werden, müssten die Schätzer zur Unterscheidung von den wahren Parametern mit einem ‚Dach‘ gekennzeichnet werden.
Also z. B. ![]() als Schätzer für den Lageparameter
als Schätzer für den Lageparameter ![]() .
.
Damit die Formeln einfach bleiben und weil keine Verwechselung auftreten kann, wird hier auf diese Notation verzichtet.
Bemerkung 2: Die genaue Darstellung der Approximation ![]() von
von ![]() ist für die weiteren Ausführungen nicht von Bedeutung, vergleiche hierzu Extremwertstatistik im Portfoliomanagement II.
ist für die weiteren Ausführungen nicht von Bedeutung, vergleiche hierzu Extremwertstatistik im Portfoliomanagement II.
Die Vorgehensweise als Ablaufplan
- Prognostiziere für die Normalverteilung die Parameter
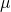 und
und 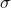 .
. - Berechne mit den Bestimmungsgleichungen
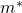 ,
, 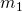 und
und 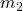 .
. - Ermittle damit die Schätzer
 und
und 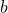 für die Parameter der Gumbel-Verteilung.
für die Parameter der Gumbel-Verteilung. - Berechne daraus den Erwartungswert und die Varianz der möglichen Vermögensminima.
Anwendung der Extremwertstatistik im Portfoliomanagement
Die folgende Grafik zeigt mit dem roten Graphen die Anpassung der Gumbel-Dichte ![]() für die Stiftung.
für die Stiftung.
Aufgetragen ist in Abbildung 1 die Gumbel-Dichte (in willkürlichen Einheiten) über dem Stiftungsvermögen in Euro.
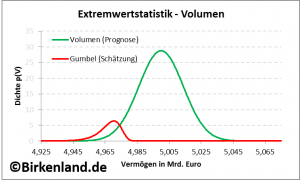
Abbildung 1: Darstellung der prognostizierten Dichte für den Volumenbestand zum Wochenschluss (grün) und die jährlichen Minima (rot).
Die Abbildung 1 zeigt außerdem die prognostizierte Dichte der Verteilung des Stiftungsvermögens (grün) um den zentralen Wert von 5 Mrd. Euro.
Es handelt sich hierbei um eine Normalverteilung, die den prognostizierten zentralen Wert von 5 Mrd. Euro als Lageparameter ![]() besitzt.
besitzt.
Ausgehend von dem Stiftungsvermögen von 5 Mrd. Euro wird prognostiziert, dass am Wochenschluss das Vermögen irgendwo innerhalb einer Bandbreite von etwa 4,94 Mrd. Euro bis 5,06 Mrd. Euro liegt. Dies entspricht in etwa dem Überdeckungsbereich der grün eingezeichneten Dichte.
Der Streuungsparameter ![]() ist rund ein Achtel kleiner als diese Bandbreite und wird zu 0,014 Mrd. Euro prognostiziert.
ist rund ein Achtel kleiner als diese Bandbreite und wird zu 0,014 Mrd. Euro prognostiziert.
Mit den zuvor notierten Bestimmungsgleichungen wurde – aus der Kenntnis von ![]() und
und ![]() , sowie von
, sowie von ![]() und
und ![]() – der Lageparameter der Gumbel-Verteilung (für
– der Lageparameter der Gumbel-Verteilung (für ![]() 52 Wochen) anhand des Modalwerts auf den Wert
52 Wochen) anhand des Modalwerts auf den Wert ![]() 4,971 Mrd. Euro geschätzt.
4,971 Mrd. Euro geschätzt.
Für den Streuungsparameter der Gumbel-Verteilung ergab die Schätzung über die Wendepunkte (bei ![]() 52 Wochen) den gerundeten Wert
52 Wochen) den gerundeten Wert ![]() 0,006 Mrd. Euro.
0,006 Mrd. Euro.
Für diese Parameter ![]() und
und ![]() überdeckt die Dichte der Gumbel-Verteilung (rot) in der Abbildung 1 einen bestimmten Wertebereich des Stiftungsvermögens und markiert damit (für die Wahl
überdeckt die Dichte der Gumbel-Verteilung (rot) in der Abbildung 1 einen bestimmten Wertebereich des Stiftungsvermögens und markiert damit (für die Wahl ![]() 52) die möglichen Lagen des minimalen Vermögenswertes im nächsten Jahr.
52) die möglichen Lagen des minimalen Vermögenswertes im nächsten Jahr.
Daraus folgt ein weiteres Ergebnis: Wenn im nächsten Jahr ein minimales Stiftungsvermögen auftritt, dann liegt dieses mit hoher Wahrscheinlichkeit irgendwo in der Bandbreite zwischen 4,94 Mrd. Euro und 4,98 Mrd. Euro.
Der Erwartungswert und die Varianz der Gumbel-Verteilung für Minimalwerte können aus den Parametern ![]() und
und ![]() der Dichte bestimmt werden:
der Dichte bestimmt werden:
![Rendered by QuickLaTeX.com \begin{flalign*} \mathrm{E}[m] & = a - b\gamma \\ \mathrm{Var}[m] & = \frac{\pi^2 b^2}{6}.\\ \end{flalign*}](http://www.birkenland.de/wp-content/ql-cache/quicklatex.com-3128e74ac1a63a945d19be321371610c_l3.png)
Hierbei ist ![]() die Euler-Mascheroni-Konstante.
die Euler-Mascheroni-Konstante.
Der Erwartungswert wird daher gerundet mit 4,968 Mrd. Euro notiert. Die Standardabweichung als Wurzel der Varianz berechnet sich gerundet zu 0,007 Mrd. Euro.
Dieses Ergebnis kann vereinfacht wie folgt interpretiert werden: Wird im kommenden Jahr ein Vermögensminimum registriert, so liegt dieses Minimum mit einer Wahrscheinlichkeit von rund 70 % in dem Bereich zwischen 4,961 Mrd. Euro und 4,975 Mrd. Euro um den Erwartungswert von 4,968 Mrd. Euro.
Nebenrechnung:
4,961 Mrd. Euro = (4,968 – 0,007) Mrd. Euro
4,975 Mrd. Euro = (4,968 + 0,007) Mrd. Euro
Das Integral über die geschätzte Dichte ![]() zwischen Unter- (4,961 Mrd. Euro) und Obergrenze (4,975 Mrd. Euro) liefert die Wahrscheinlichkeit von rund 70 %.
zwischen Unter- (4,961 Mrd. Euro) und Obergrenze (4,975 Mrd. Euro) liefert die Wahrscheinlichkeit von rund 70 %.
Damit ist für die Stiftung auf Jahressicht die Wahrscheinlichkeit für das Auftreten eines Vermögensminimums in diesem Wertebereich bemessen.
Die Eintrittswahrscheinlichkeit für den Schaden, dass überhaupt ein Vermögensminimum kleiner oder gleich dem Modalwert auftritt, kann in gleicher Weise durch Integration von ![]() vom linken Rand – bei minus Unendlich – bis zum Modalwert berechnet werden und liegt hier bei unter 1 %. Letzteres entspricht dem Wert der Normalverteilungsfunktion
vom linken Rand – bei minus Unendlich – bis zum Modalwert berechnet werden und liegt hier bei unter 1 %. Letzteres entspricht dem Wert der Normalverteilungsfunktion ![]() an der Stelle des Modalwerts.
an der Stelle des Modalwerts.
Vergleiche hierzu auch die Endergebnisse aus dem Beitrag Extremwertstatistik im Portfoliomanagement.
Extremwertstatistik im Portfoliomanagement: Risikobewertung im Risikoreport
Auf Basis der zuvor abgeleiteten Ergebnisse würde die Risikoprognose zur Entwicklung des Stiftungsvermögens im kommenden Jahr den Erwartungswert zu Grunde legen.
Wir zeigen eine mögliche (Kurz-)Darstellung der Ergebnisse im kombinierten Risikoreport / Steuerungsreport.
Risikoreport / Steuerungsreport – Auszug
Im Risikoreport des Risikomanagements für das Stiftungsvermögen könnte – nach der Darstellung der getätigten Näherungen und Annahmen – im einfachsten Fall folgende Formulierung stehen:
Die Modellprognose und die Prognose der Modellparameter für die Vermögensbestände zum Wochenschluss führen zu folgender Risikoeinschätzung: Wenn im kommenden Jahr ein minimales Vermögen auftritt, dann dürfte es in der Nähe des Erwartungswertes bei etwa 4,968 Mrd. Euro liegen.
Abhängig vom gewünschten Detailgrad können bei Bedarf alle Analyseergebnisse (Vermögensminimum, Wertebereich der Schwankung, Eintrittswahrscheinlichkeit, etc.) in den Risikoreport als Bestandteil der Risikoprognose integriert werden.
Je nachdem, ob diese Risikoprognose im Einklang mit den Vorgaben in den Anlagerichtlinien steht oder nicht, muss gegebenenfalls die Zusammensetzung des Portfolios neu gestaltet werden.
Entsprechende Handlungsempfehlungen (inkl. Notfallmaßnahmen) für das Portfoliomanagement sind ebenfalls im Report zu dokumentieren.
Häufigkeit des Risikoreports / Steuerungsreports
Abweichend von gesetzlichen Vorgaben wird vom institutionellen Anleger die Häufigkeit eines kombinierten Reports über das Management seines Anlageportfolios mit zunehmender Höhe des Anlagekapitals – im Vergleich zu seinem Gesamtvermögen – und mit zunehmender Höhe des eingegangenen Anlagerisikos größer gewählt werden.
Die Erfahrung zeigt, dass bei einem kleineren Anteil am Gesamtvermögen und risikoaverser Anlagepolitik die gesetzlich vorgeschriebene Häufigkeit dem Anleger oftmals ausreichend erscheint, wogegen er bei größeren Anteilen und risikosuchender Anlagepolitik – so wie im Beispiel der Stiftung – eher die wöchentliche Berichterstattung bevorzugt.
Extremwertstatistik im Portfoliomanagement: Güte der Ergebnisse
Es stellt sich abschließend die Frage, wie gut sind diese Ergebnisse?
Bei größeren Datenbeständen stehen mehrere Möglichkeiten zur Verfügung, um die Güte der Anpassung zu bewerten.
Die möglichen Gütetests lassen sich dabei in zwei Gruppen einteilen.
Zum einen sind dies die quantitativen Anpassungstests, die eher auf einer formalen Vorgehensweise beruhen und zur Anwendung auf empirischen Daten konzipiert sind.
Davon zu unterscheiden sind die qualitativen Anpassungstests, die überwiegend auf optische, vergleichende Bewertungsmaßstäbe setzen.
Da keine empirischen Daten vergangener Entwicklungen des Anlagevermögens vorliegen, sind weder die quantitativen Anpassungstests
- Chi-Quadrat-Test
- Cramér-von-Mises-Test
- Anderson-Darling-Test
- Kullback-Leibler-Divergenz
- Akaike-Informationskriterium
- Kolmogorow-Smirnow-Test
noch die qualitativen Anpassungstests (PP- und QQ-Plots) anwendbar.
Es besteht aber die Möglichkeit, den Funktionsverlauf der geschätzten Dichte ![]() qualitativ zu bewerten.
qualitativ zu bewerten.
Dazu wird ein optischer Vergleich der geschätzten Dichte ![]() gegenüber der approximierten Dichte
gegenüber der approximierten Dichte ![]() und einer durch Monte Carlo Simulation erhaltenen Dichte
und einer durch Monte Carlo Simulation erhaltenen Dichte ![]() durchgeführt.
durchgeführt.
Bemerkung: Zur Konstruktion und zur formalen Darstellung von ![]() vergleiche Extremwertstatistik im Portfoliomanagement II.
vergleiche Extremwertstatistik im Portfoliomanagement II.
Im Rahmen der Monte Carlo Simulation wurden 10.000 Vermögensminima mit der prognostizierten Verteilung ![]() des Vermögensbestandes erzeugt.
des Vermögensbestandes erzeugt.
Anschließend wurde die Maximum-Likelihood-Methode verwendet, um aus den Vermögensminima die Parameter ![]() und
und ![]() der Gumbel-Verteilung
der Gumbel-Verteilung ![]() zu bestimmen.
zu bestimmen.
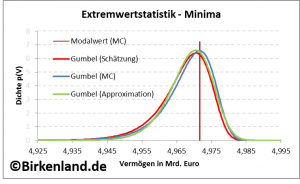
Die folgende Abbildung zeigt den optischen Vergleich der drei Dichten.
Die Abbildung 2 zeigt als rote Kurve die mit unserem Verfahren geschätzte Gumbel-Dichte ![]() im Vergleich zu der Approximation
im Vergleich zu der Approximation ![]() (grün) für
(grün) für ![]() 52 Wochen.
52 Wochen.
Zusätzlich eingezeichnet ist die simulierte Dichte ![]() in blau, sowie der simulierte Modalwert (weinrot).
in blau, sowie der simulierte Modalwert (weinrot).
Es ist zu erkennen, dass alle drei Dichten sehr eng übereinander liegen und nahezu den gleichen Modalwert besitzen.
Diese Beobachtung kann mathematisch durch Verwendung von speziellen Tests – auf der Basis der zuvor erwähnten Anpassungstests – quantifiziert werden. Stark vereinfacht geht es im Kern dabei darum, auf einem vorgewählten Signifikanzniveau nachzuweisen, dass die drei gezeigten Dichten „das gleiche Phänomen“ beschreiben.
Wegen der erkennbar nahezu perfekten Deckung der Dichten untereinander – die eine fast gleiche Lage der Dichten anzeigt – reicht uns die optische Einwertung an dieser Stelle aus.
Insgesamt können wir aus dem optischen Vergleich schlussfolgern, dass die Vermögensminima gut durch unsere geschätzte Dichte ![]() der Gumbel-Verteilung für Minima statistisch beschrieben werden.
der Gumbel-Verteilung für Minima statistisch beschrieben werden.
Einwertung
Die zuvor skizzierte ungewöhnliche Ausgangslage, dass keine Daten über vergangene Entwicklungen des Anlagevermögens vorliegen, tritt einerseits in der besonderen Situation auf, dass das Anlageportfolio neu aufgesetzt worden ist.
Aber auch ein abrupter Wechsel des Portfoliomanagements, der Portfolioausrichtung und/oder der Anlagerichtlinien kann zu einer derartigen besonderen Situation führen, dass keine Daten für eine nach vorne gerichtete Risikobewertung vorliegen.
Das hier vorgeschlagene systematische Verfahren zur Risikobewertung gestattet unter diesen Umständen auf der Basis von Prognosen eine erste, indikative Einschätzung des zu erwartenden Risikos mit Blick auf das mögliche Vermögensminimum in einem gewählten künftigen Zeitraum.
Die Endergebnisse sind jedoch im individuellen Einzelfall kritisch zu prüfen und anhand weiterer Informationen zu validieren.
Wahl des Prognosehorizonts
Zum Zeitpunkt der Neugestaltung eines Anlageportfolios liefert das hier vorgestellte Verfahren eine wertvolle Ersteinschätzung des Risikos hinsichtlich eines möglichen künftigen Vermögensminimums.
Günstigerweise sollte das Verfahren für eine enge und zügige Risikoaussteuerung auf den nahen unterjährigen Zeitraum abstellen. Es ist daher wenig zielführend, den Prognosehorizont deutlich über ein Jahr (![]() 52) zu wählen.
52) zu wählen.
Der Risikoreport sollte also statt zu langer eher kürzere, unterjährige Fristen enthalten.
Bewährt hat sich hier die kombinierte Wahl von drei, sechs und zwölf Monaten, d. h. Zeiträume von ![]() 12, 24 und 52 Wochen.
12, 24 und 52 Wochen.
Verfahrensanpassung im Zeitverlauf
Bei einer engmaschigen Kontrolle der Vermögensbestände – beispielsweise wöchentlich – wird rasch eine ausreichende Datenbasis zur Verfügung stehen, so dass dann die Risikobewertung mit dem Verfahren aus unserem Beitrag Extremwertstatistik im Portfoliomanagement II erfolgen kann.
So ist mit dem Wechsel des Verfahrens beispielsweise bereits auf der Basis von ![]() 12 Wochen eine valide, datengestützte Risikobewertung für die folgenden drei Monate möglich.
12 Wochen eine valide, datengestützte Risikobewertung für die folgenden drei Monate möglich.
Backtest, Validierung und Anpassung
Im Verlauf der ersten drei Monaten wird bereits eine kleine Datenbasis aufgebaut, so dass das hier beschriebene Verfahren und die daraus abgeleiteten Risikoprognosen in diesem Anwendungszeitraum fortlaufend einer Überprüfung im Rahmen eines Backtestings unterzogen werden können.
Führt die Validierung zu notwendigen Anpassungen – beispielsweise hinsichtlich der Verteilungsannahme – so sind entsprechenden Anpassungen umgehend durchzuführen und in der Änderungsdokumentation zum Prozess zu protokollieren.
Prognoseunsicherheit und Prognoserisiko
Die Aussagekraft des Verfahrens hängt entscheidend von der Qualität der Prognose der Parameter ab. Hier: von ![]() und
und ![]() der Verteilungsfunktion
der Verteilungsfunktion ![]() .
.
Üblicherweise würde zur Abschätzung des Einflusses der Prognoseunsicherheit auf die Risikobewertung ein statistisches Modell für die Parameter berücksichtigt werden, um so eine mögliche Unterschätzung des Risikos zu überprüfen und zu berücksichtigen.
Eine rasche, erste Abschätzung gelingt, wenn die Bandbreiten der Prognosen ![]() bzw.
bzw. ![]() analysiert werden.
analysiert werden.
Ein deutlich kleineres Vermögensminimum wird sicher dann angenommen, wenn gilt: ![]() und
und ![]() .
.
D. h., wenn der Ertrag kleiner und die Streuung größer als ursprünglich prognostiziert ausfallen.
Dies ist ein angenommener schlimmster Prognosefehler, der ein erheblich kleineres Vermögensminimum als Risikobewertung erwarten lässt.
Mit den neuen Parametern ![]() und
und ![]() wird das in diesem Beitrag vorgestellte Verfahren nochmals angewendet und der neue Erwartungswert des Vermögensminimums berechnet.
wird das in diesem Beitrag vorgestellte Verfahren nochmals angewendet und der neue Erwartungswert des Vermögensminimums berechnet.
Der Wert dieses neuen Vermögensminimums im Vergleich zu dem zuvor berechneten alten Vermögensminimum gibt eine erste Indikation über den Einfluss der Prognoseunsicherheit.
Aus der Prognoseunsicherheit erwächst ein Prognoserisiko, dass sich also als mögliche Fehlbewertung des Marktrisikos zeigen kann.
Die Möglichkeit und der abgeschätzte Umfang der Fehlbewertung sollte ebenfalls als Grenze des Verfahrens in einem Fachkonzept dokumentiert werden.
Um abschließend den Einfluss der Prognoseunsicherheit zu mildern, kann das hier vorgestellte Verfahren mit dem von uns entwickelten Konzept der Konservativen Risikobewertung kombiniert werden.
Szenarioanalyse und Stresstest
Ganz allgemein können mit dem zuvor ausgearbeiteten Verfahren sämtliche Belange einer Szenarioanalyse und eines aufgeprägten Stresstests berücksichtigt werden.
Das wird möglich, wenn die entsprechenden Vorgaben in dem Risikomodell beispielsweise in den Parametern ![]() und
und ![]() abgebildet werden und die Risikobewertung in jedem Szenario oder Stressfall erneut vorgenommen wird.
abgebildet werden und die Risikobewertung in jedem Szenario oder Stressfall erneut vorgenommen wird.
Extremwertstatistik im Portfoliomanagement: Literatur
Extremwerttheorie
http://wwwmath.uni-muenster.de/statistik/kabluchko/Skripte/Skript_Extremwerttheorie.pdf
Extremwertstatistik zur Modellbildung
Modelling Extremal Events: for Insurance and Finance
(Embrecht, Klüppelberg, Mikosch im Springer-Verlag, 2001)
Theorie der Extremwertstatistik
https://wwwmath.uni-muenster.de/statistik/loewe/extrem.pdf
Über die Extremwertstatistik und Wiederkehrintervalle in langzeitkorrelierten Systemen
http://www.physik.uni-halle.de/Fachgruppen/kantel/PhD_Eichner.pdf
Ermittlung des Value-at-Risk von Finanzportefeuilles mit Methoden der Extremwertstatistik
http://www.risknet.de/fileadmin/eLibrary/Extremwerttheorie-Diplomarbeit-Frahm.pdf

Vermögensanlage: When the Going Gets Tough – Was tun in schwierigen Zeiten? « LGT Finanzblog
[…] Wer Weitergehendes zum Risikomanagement im Portfoliomanagement sucht, findet auf Birkenland einen Beitrag: Extremwertstatistik im Portfolio-Management […]
Vermögensanlagen und Risikoverhalten - LGT Finanzblog
[…] Wer Weitergehendes zum Risikomanagement im Portfoliomanagement sucht, findet auf Birkenland einen Beitrag: Extremwertstatistik im Portfolio-Management […]