Wie ein Portfoliomanager mit der Linearumsetzungsstrategie II ein 5 Milliarden Euro Portfolio marktschonend umschichten kann.
Im ersten Beitrag zur Linearumsetzungsstrategie wurden bereits die grundsätzlichen Probleme beschrieben, die große institutionelle Adressen haben, wenn sie Kapitalvolumen von mehreren Milliarden Euro in ihrem Anlageportfolio zwischen verschiedenen Vermögenswerten umschichten müssen.
Ein wesentliches Problem war, dass der Portfoliomanager beim großvolumigen Kauf oder Verkauf von Vermögenswerten den Preis an den Kapitalmärkten beeinflusst und die letzten Wertpapiere gegebenenfalls zu einem schlechteren Preis handelt.
Einen Ausweg zur Vermeidung dieses Effektes bietet die bereits beschriebene Linearumsetzungsstrategie I. Diese zielt darauf ab, sukzessive – beispielsweise im Wochenrhythmus – das Anlagevermögen in jeweils gleichen Teilvolumina umzuschichten.
Bei der Gestaltung der Linearumsetzungsstrategie war der Aspekt der Automatisierbarkeit wichtig. Diese führt bei einer zeitlich äquidistanten und zudem noch volumengleichen Ausgestaltung der automatischen Umschichtung zu dem Problem, dass andere Marktteilnehmer nach kurzer Zeit die Systematik erkennen und sich entsprechend mit ihren Transaktionen vorpositionieren können.
Damit könnte der Nachteil verbunden sein, dass der Portfoliomanager seine Tranche nur zu schlechteren Preisen handeln kann.
Die hier nun vorgestellte zweite Variante der Linearumsetzungsstrategie mildert dieses Problem dadurch, dass beispielsweise pro Woche nach festen Regeln jeweils unterschiedliche Teilvolumen berechnet und im Anlageportfolio umgeschichtet werden.
Artikelübersicht
Nach der Grundidee wird die Theorie der Linearumsetzungsstrategie II vorgestellt. Anschließend wird die zentrale Geleichung der Linearumsetzungsstrategie II im Detail hergeleitet. Anhand eines Beispiels wird zum Abschluss die Anwendung der Linearumsetzungsstrategie II gezeigt.
Grundidee der Linearumsetzungsstrategie II
Es wird wie bei der Linearumsetzungsstrategie I wieder angenommen, dass sich das Ausgangsportfolio durch den ![]() -dimensionalen Gewichtsvektor
-dimensionalen Gewichtsvektor ![]() und das Zielportfolio durch den
und das Zielportfolio durch den ![]() -dimensionalen Gewichtsvektor
-dimensionalen Gewichtsvektor ![]() darstellen lassen. Wobei für beide Gewichtsvektoren die Nebenbedingung gilt, dass die Summe der Einzelgewichte gleich 100% beträgt. Mit der Indikatoreins lässt sich diese Nebenbedingung in der Form
darstellen lassen. Wobei für beide Gewichtsvektoren die Nebenbedingung gilt, dass die Summe der Einzelgewichte gleich 100% beträgt. Mit der Indikatoreins lässt sich diese Nebenbedingung in der Form ![]() bzw.
bzw. ![]() ausdrücken.
ausdrücken.
Die Endpunkte beider Gewichtsvektoren liegen im ![]() -dimensionalen Raum auf einer
-dimensionalen Raum auf einer ![]() -dimensionalen Hyperfläche. Diese Hyperfläche ist per Konstruktion ein konvexes Gebiet
-dimensionalen Hyperfläche. Diese Hyperfläche ist per Konstruktion ein konvexes Gebiet ![]() , so dass zwischen den Gewichtsvektoren des Ausgangs- und Zielportfolios eine Verbindungsstrecke existiert, die vollständig in
, so dass zwischen den Gewichtsvektoren des Ausgangs- und Zielportfolios eine Verbindungsstrecke existiert, die vollständig in ![]() liegt, vgl. hierzu auch die Ausführungen zur Linearumsetzungsstrategie I.
liegt, vgl. hierzu auch die Ausführungen zur Linearumsetzungsstrategie I.
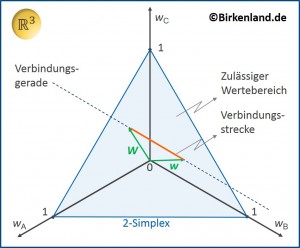
Die Abbildung 1 verdeutlicht diesen Sachverhalt für ![]() = 3 Vermögenswerte, hier bezeichnet mit
= 3 Vermögenswerte, hier bezeichnet mit ![]() und
und ![]() .
.
Hier ist der Fall dargestellt, dass die einzelnen Vermögenswerte Anteile (![]() und
und ![]() ) zwischen 0% und 100% im Portfolio annehmen können, so dass der zulässige Wertebereich sich als ein spezielles konvexes Gebiet – dem sogenannten 2-Simplex – im
) zwischen 0% und 100% im Portfolio annehmen können, so dass der zulässige Wertebereich sich als ein spezielles konvexes Gebiet – dem sogenannten 2-Simplex – im ![]() darstellen lässt.
darstellen lässt.
Ebenfalls eingezeichnet ist die Verbindungsgerade durch die Endpunkte der Gewichtsvektoren für das Ausgangs- und Zielportfolio. Die Verbindungsstrecke zwischen den Endpunkten – als Teil der Verbindungsgeraden – liegt vollständig in dem 2-Simplex.
Die Linearumsetzungsstrategie II verfolgt die Grundidee, dass der Ausgangsvektor durch eine Drehung auf den Zielvektor abgebildet wird.
Die Pfeilspitze des Ausgangsvektors beschreibt dabei einen Kreisbogen über der Verbindungsstrecke.
Das Besondere der Linearumsetzungsstrategie II ist, dass die vollständige Drehung des Ausgangsvektors entlang des Kreisbogens in ![]() einzelnen Teilschritten (z.B. im Wochenrhythmus) vollzogen wird.
einzelnen Teilschritten (z.B. im Wochenrhythmus) vollzogen wird.
Zu jedem Teilschritt erfolgt eine auf den Ursprung gerichtete Zentralprojektion der Pfeilspitze des gedrehten Ausgangvektors auf die Verbindungsstrecke. Somit lassen sich die zugehörenden Gewichtsvektoren ![]() für
für ![]() berechnen.
berechnen.
Diese Gewichtsvektoren sind also das Ergebnis einer Drehung und anschließenden Projektion, sie führen vom Ursprung zu dem Projektionspunkt auf der Verbindungsstrecke und erfüllen die Nebenbedingung ![]() für jedes
für jedes ![]() .
.
Die Ergebnisvektoren ![]() jeder Einzeldrehung beschreiben die Zusammensetzung des Portfolios nach dem entsprechenden Teilschritt (z.B. in der
jeder Einzeldrehung beschreiben die Zusammensetzung des Portfolios nach dem entsprechenden Teilschritt (z.B. in der ![]() -ten Woche).
-ten Woche).
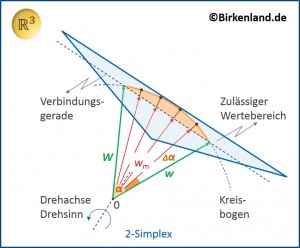
Die Abbildung 2 zeigt die Drehung und die Projektion für den Fall ![]() = 3 Vermögenswerte im Detail.
= 3 Vermögenswerte im Detail.
In diesem Beispiel wird die Drehung entlang des Kreisbogens in ![]() = 5 Teilschritten vollzogen.
= 5 Teilschritten vollzogen.
Der 2-Simplex ist in dieser Darstellung leicht geneigt, so dass das Profil des Kreisbogens, die einzelnen Projektionen und die Lage der zugehörigen Gewichtsvektoren ![]() erkennbar werden.
erkennbar werden.
Die Drehung ![]() erfolgt im
erfolgt im ![]() in einer Ebene, die als Drehebene bezeichnet wird.
in einer Ebene, die als Drehebene bezeichnet wird.
Spezielle im ![]() verläuft senkrecht zu dieser Drehebene durch den Ursprung die Drehachse. Um diese Drehachse wird der Gewichtsvektor für das Ausgangsportfolio in Richtung Gewichtsvektor für das Zielportfolio gedreht. Die Abbildung 2 zeigt diese Drehung um die eingezeichnete Drehachse.
verläuft senkrecht zu dieser Drehebene durch den Ursprung die Drehachse. Um diese Drehachse wird der Gewichtsvektor für das Ausgangsportfolio in Richtung Gewichtsvektor für das Zielportfolio gedreht. Die Abbildung 2 zeigt diese Drehung um die eingezeichnete Drehachse.
Bemerkung: Die Drehachse ist im ![]() die sogenannte Fixpunktgerade, die unter der Drehung auf sich selbst abgebildet wird.
die sogenannte Fixpunktgerade, die unter der Drehung auf sich selbst abgebildet wird.
Die Theorie zur Linearumsetzungsstrategie II
Die nachfolgenden Ausführungen haben das Ziel, die ![]() -dimensionalen Gewichtsvektoren
-dimensionalen Gewichtsvektoren ![]() in den einzelnen Teilschritten
in den einzelnen Teilschritten ![]() eindeutig zu berechnen.
eindeutig zu berechnen.
Die Berechnung der Gewichtsvektoren ![]() hängt bei der Linearumsetzungsstrategie II nur von dem Gewichtsvektor des Ausgangsportfolios
hängt bei der Linearumsetzungsstrategie II nur von dem Gewichtsvektor des Ausgangsportfolios ![]() und vom Gewichtsvektor für das Zielportfolio
und vom Gewichtsvektor für das Zielportfolio ![]() , sowie der Vorgabe der Anzahl der Teilschritte
, sowie der Vorgabe der Anzahl der Teilschritte ![]() ab.
ab.
Damit ist die Linearumsetzungsstrategie II für Portfolios mit beliebig vielen Vermögensanlagen in automatisierten Handelssystemen implementierbar.
Drehung in der 2-dimensionalen Ebene
Ausgangspunkt der Herleitung ist die Feststellung, dass die beiden Gewichtsvektoren ![]() und
und ![]() im
im ![]() -dimensionalen Vektorraum eine 2-dimensionale Drehebene als Unterraum des
-dimensionalen Vektorraum eine 2-dimensionale Drehebene als Unterraum des ![]() aufspannen.
aufspannen.
Die Drehung selbst ist eine spezielle lineare Abbildung im ![]() und kann durch eine Drehmatrix
und kann durch eine Drehmatrix ![]() dargestellt werden.
dargestellt werden.
Durch Multiplikation eines Vektors ![]() mit der Drehmatrix
mit der Drehmatrix ![]() wird ein gegenüber
wird ein gegenüber ![]() gedrehter Ergebnisvektor
gedrehter Ergebnisvektor ![]() erzeugt:
erzeugt: ![]() .
.
Bemerkung: Die Fixpunktgerade als Drehachse wird im ![]() durch einen Vektor
durch einen Vektor ![]() beschrieben, der Lösung folgender Gleichung ist:
beschrieben, der Lösung folgender Gleichung ist: ![]() Der Vektor
Der Vektor ![]() wird also durch die Drehung nicht verändert. Im
wird also durch die Drehung nicht verändert. Im ![]() -dimensionalen Fall gibt es mehrere Vektoren, die diese Gleichung erfüllen, so dass nicht von einer ausgezeichneten Drehachse ausgegangen werden kann. Allgemein wird daher von einer Drehung in der 2-dimensionalen Drehebene gesprochen, die durch
-dimensionalen Fall gibt es mehrere Vektoren, die diese Gleichung erfüllen, so dass nicht von einer ausgezeichneten Drehachse ausgegangen werden kann. Allgemein wird daher von einer Drehung in der 2-dimensionalen Drehebene gesprochen, die durch ![]() und
und ![]() aufgespannt wird.
aufgespannt wird.
Bestimmung der infinitesimalen Drehmatrix
Zunächst werden die Einheitsvektoren in Richtung der vorgegebenen Gewichtsvektoren ![]() und
und ![]() berechnet:
berechnet:
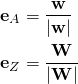
Bemerkung: Der Ausdruck ![]() bezeichnet den Betrag des Vektors
bezeichnet den Betrag des Vektors ![]() . Für den Betrag von Einheitsvektoren gilt:
. Für den Betrag von Einheitsvektoren gilt: ![]() Vereinfacht ausgedrückt: Einheitsvektoren haben die Länge 1.
Vereinfacht ausgedrückt: Einheitsvektoren haben die Länge 1.
Mit ![]() ist der Einheitsvektor in Richtung des Gewichtsvektors des Ausgangsportfolios beschrieben, während
ist der Einheitsvektor in Richtung des Gewichtsvektors des Ausgangsportfolios beschrieben, während ![]() den entsprechenden Vektor für das Zielportfolio bezeichnet.
den entsprechenden Vektor für das Zielportfolio bezeichnet.
Aus diesen beiden Einheitsvektoren werden nun durch Anwendung des Gram-Schmidtschen Orthogonalisierungsverfahrens zwei orthogonale Einheitsvektoren ![]() und
und ![]() berechnet, die ebenfalls in der von
berechnet, die ebenfalls in der von ![]() und
und ![]() aufgespannten Drehebene liegen.
aufgespannten Drehebene liegen.
- Orthogonalisieren:
![]()
- Normalisieren:
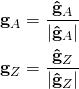
Bemerkung: Der Ausdruck ![]() bezeichnet das Skalarprodukt (Zeilenvektor
bezeichnet das Skalarprodukt (Zeilenvektor ![]() Spaltenvektor) der beiden Vektoren.
Spaltenvektor) der beiden Vektoren.
Die normierten, orthogonalen Einheitsvektoren ![]() und
und ![]() bilden eine Orthonormalbasis der 2-dimensionalen Drehebene.
bilden eine Orthonormalbasis der 2-dimensionalen Drehebene.
Damit lässt sich die Erzeugende ![]() einer infinitesimalen Drehung in der Drehebene angeben:
einer infinitesimalen Drehung in der Drehebene angeben:
![]()
Bemerkung: Der Ausdruck ![]() bezeichnet das dyadische bzw. tensorielle Produkt (Spaltenvektor
bezeichnet das dyadische bzw. tensorielle Produkt (Spaltenvektor ![]() Zeilenvektor) der beiden Vektoren.
Zeilenvektor) der beiden Vektoren.
Die Erzeugende ![]() der infinitesimalen Drehung ist eine reelle
der infinitesimalen Drehung ist eine reelle ![]() Matrix, mit
Matrix, mit ![]() Zeilen und
Zeilen und ![]() Spalten, d.h.
Spalten, d.h. ![]() .
.
Damit ist schließlich die infinitesimale Drehmatrix ![]() für einen infinitesimalen Drehwinkel
für einen infinitesimalen Drehwinkel ![]() über folgenden Zusammenhang gegeben:
über folgenden Zusammenhang gegeben:
![]()
Bemerkung: Die Matrix ![]() bezeichnet die Einheitsmatrix in
bezeichnet die Einheitsmatrix in ![]() . Die Diagonaleinträge der Einheitsmatrix
. Die Diagonaleinträge der Einheitsmatrix ![]() haben jeweils den Wert 1, alle anderen Einträge den Wert 0.
haben jeweils den Wert 1, alle anderen Einträge den Wert 0.
Die infinitesimale Drehung
Durch die Matrixmultiplikation ![]() (Matrix
(Matrix ![]() Spaltenvektor) wird ein neuer (Spalten-)Vektor
Spaltenvektor) wird ein neuer (Spalten-)Vektor ![]() erzeugt, der gegenüber dem Gewichtsvektor
erzeugt, der gegenüber dem Gewichtsvektor ![]() des Ausgangsportfolios um einen infinitesimalen Winkel
des Ausgangsportfolios um einen infinitesimalen Winkel ![]() in Richtung des Gewichtsvektors
in Richtung des Gewichtsvektors ![]() für das Zielportfolio gedreht wurde.
für das Zielportfolio gedreht wurde.
Um die vollständige Drehung durchführen zu können, wird zunächst der Winkel zwischen den beiden Gewichtsvektoren ![]() und
und ![]() bestimmt.
bestimmt.
Drehwinkel in der Drehebene
Die beiden Gewichtsvektoren ![]() und
und ![]() und damit auch die beiden zugehörigen Einheitsvektoren
und damit auch die beiden zugehörigen Einheitsvektoren ![]() und
und ![]() schließen einen Winkel
schließen einen Winkel ![]() in der Drehebene ein.
in der Drehebene ein.
Bei der Drehung muss der Vektor ![]() um diesen Winkel
um diesen Winkel ![]() in der Drehebene gedreht werden, damit er in die Richtung des Gewichtsvektors
in der Drehebene gedreht werden, damit er in die Richtung des Gewichtsvektors ![]() für das Zielportfolio zeigt.
für das Zielportfolio zeigt.
Mit den zuvor berechneten Einheitsvektoren ![]() und
und ![]() ist der Drehwinkel
ist der Drehwinkel ![]() gegeben durch folgenden Zusammenhang:
gegeben durch folgenden Zusammenhang:
![]()
Bemerkung: Für die weiteren Berechnungen wird ![]() in Radiant benötigt.
in Radiant benötigt.
Die Matrixexponentialdarstellung der Linearumsetzungsstrategie II
Der infinitesimale Drehwinkel ![]() kann durch die Ersetzung
kann durch die Ersetzung ![]() für große Werte von
für große Werte von ![]() abgeschätzt werden. Durch diese Ersetzung wird der infinitesimale Drehwinkel approximiert und entspricht für große Werte von
abgeschätzt werden. Durch diese Ersetzung wird der infinitesimale Drehwinkel approximiert und entspricht für große Werte von ![]() einem kleinen Teildrehwinkel.
einem kleinen Teildrehwinkel.
Werden nun ![]() einzelne Drehungen hintereinander durchgeführt, so wird die Drehung des Gewichtsvektors für das Ausgangsportfolio um den Winkel
einzelne Drehungen hintereinander durchgeführt, so wird die Drehung des Gewichtsvektors für das Ausgangsportfolio um den Winkel ![]() vollzogen.
vollzogen.
Das Durchführen von ![]() einzelnen Drehungen bedeutet eine
einzelnen Drehungen bedeutet eine ![]() -fache Multiplikation des Gewichtsvektors mit der infinitesimalen Drehmatrix.
-fache Multiplikation des Gewichtsvektors mit der infinitesimalen Drehmatrix.
Durch ![]() -faches Multiplizieren des Gewichtsvektor
-faches Multiplizieren des Gewichtsvektor ![]() für das Ausgangsportfolio mit der infinitesimalen Drehmatrix
für das Ausgangsportfolio mit der infinitesimalen Drehmatrix ![]() wird ein Ergebnisvektor
wird ein Ergebnisvektor ![]() erzeugt, der in die Richtung des Gewichtsvektors des Zielportfolios zeigt:
erzeugt, der in die Richtung des Gewichtsvektors des Zielportfolios zeigt:
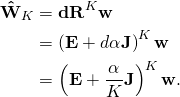
Wird nun die Anzahl ![]() der Teildrehwinkel stetig erhöht und strebt im Grenzprozess gegen Unendlich, dann wird der Ausdruck vor dem Gewichtsvektor
der Teildrehwinkel stetig erhöht und strebt im Grenzprozess gegen Unendlich, dann wird der Ausdruck vor dem Gewichtsvektor ![]() gleich dem Matrixexponential und es gilt:
gleich dem Matrixexponential und es gilt:
![]()
Da das Matrixexponential ![]() wieder auf eine Matrix
wieder auf eine Matrix ![]() führt, gilt folgende lineare Abbildung:
führt, gilt folgende lineare Abbildung:
![]()
Hierbei ist ![]() die Drehmatrix, die den Gewichtsvektor des Ausgangsportfolios um den Winkel
die Drehmatrix, die den Gewichtsvektor des Ausgangsportfolios um den Winkel ![]() in die Richtung des Gewichtsvektors des Zielportfolios dreht.
in die Richtung des Gewichtsvektors des Zielportfolios dreht.
Dieser Ergebnisvektor ![]() erfüllt zwar noch nicht die Nebenbedingung, dass die Summe aller Einträge gleich 100% ergibt, aber er liegt parallel zum Gewichtsvektor
erfüllt zwar noch nicht die Nebenbedingung, dass die Summe aller Einträge gleich 100% ergibt, aber er liegt parallel zum Gewichtsvektor ![]() des Zielportfolios.
des Zielportfolios.
Nach der Drehung gilt also ![]() .
.
Wird abschließend ![]() berechnet, so erfüllt
berechnet, so erfüllt ![]() die Nebenbedingung
die Nebenbedingung ![]() und entspricht dem Gewichtsvektor
und entspricht dem Gewichtsvektor ![]() des Zielportfolios.
des Zielportfolios.
Nach der Skalierung gilt also ![]() .
.
Zentrale Gleichung der Linearumsetzungsstrategie II
In der Formulierung ![]() kann die Drehung um den Winkel
kann die Drehung um den Winkel ![]() in
in ![]() Teilschritten mit kleineren Winkeln
Teilschritten mit kleineren Winkeln ![]() vollzogen werden.
vollzogen werden.
Wenn für ![]() gilt:
gilt: ![]() (also der Gewichtsvektor für das Ausgangsportfolio ist der Startvektor der Drehung), dann berechnen sich die Vektoren der Teilschritt für
(also der Gewichtsvektor für das Ausgangsportfolio ist der Startvektor der Drehung), dann berechnen sich die Vektoren der Teilschritt für ![]() über folgende Rekursionsformel:
über folgende Rekursionsformel:
![]()
Hier wird durch Skalieren mit dem Nenner ![]() erreicht, dass der gedrehte Vektor
erreicht, dass der gedrehte Vektor ![]() die Nebenbedingung
die Nebenbedingung ![]() sofort erfüllt.
sofort erfüllt.
Die oben abgeleitete Rekursionsformel ist die Matrixexponentialdarstellung der Linearumsetzungsstrategie II.
Wird zur Abkürzung die Ersetzung ![]() eingeführt, so folgt die zentrale Gleichung der Linearumsetzungsstrategie II:
eingeführt, so folgt die zentrale Gleichung der Linearumsetzungsstrategie II:
![]()
Sukzessive Gewichtsverschiebung
Die Veränderung der Gewichtung der Vermögensanlagen von Teilschritt zu Teilschritt ist gleich der Differenz ![]() .
.
Programmierung der Linearumsetzungsstrategie II
Pseudo-Code zur Umsetzung in EDV-Programmen:
- Vorgabe der Gewichtsvektoren
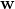 und
und 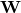 , sowie der Anzahl der Teilschritte
, sowie der Anzahl der Teilschritte 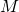 .
. - Berechnung der Einheitsvektoren
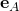 und
und 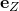 .
. - Daraus Bestimmung der Orthonormalbasis (
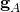 und
und 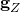 ) der Drehebene und mit der Orthonormalbasis erfolgt die Berechnung der Erzeugenden
) der Drehebene und mit der Orthonormalbasis erfolgt die Berechnung der Erzeugenden 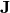 der infinitesimalen Drehung.
der infinitesimalen Drehung. - Berechnung des Winkels
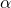 zwischen den Gewichtvektoren, sowie
zwischen den Gewichtvektoren, sowie 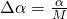 für die Teildrehungen.
für die Teildrehungen. - Mit
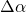 und
und 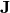 wird anschließend das Matrixexponential
wird anschließend das Matrixexponential 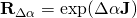 berechnet.
berechnet. - Setze
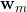 für
für 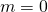 gleich dem Gewichtsvektor für das Ausgangsportfolio, also
gleich dem Gewichtsvektor für das Ausgangsportfolio, also 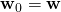 .
. - Berechne
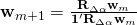 und den Differenzvektor
und den Differenzvektor 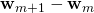 .
. - Wiederhole Schritt 7 solange bis
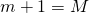 gilt.
gilt.
Bemerkung: Das Matrixexponential ist eine Funktion und muss in der Linearumsetzungsstrategie II lediglich einmal zu Beginn berechnet werden. Das kann bspw. online auf der Internetpräsenz von WolframAlpha durchgeführt werden, wenn das verwendete Programmpaket die Auswertung des Matrixexponential nicht unterstützt.
Handhabung der Linearumsetzungsstrategie II
Die Anwendung der Linearumsetzungsstrategie II erfordert als einzigen zusätzlichen Eingabeparameter die vorher festgelegte Anzahl der Teilschritte ![]() .
.
Zur Festlegung der Anzahl ![]() wird die Formel der Linearumsetzungsstrategie I zur Berechnung des Umschichtungsvolumens pro Teilschritt genutzt:
wird die Formel der Linearumsetzungsstrategie I zur Berechnung des Umschichtungsvolumens pro Teilschritt genutzt:
![]() .
.
Die Berechnungsvorschrift ![]() bildet die sogenannte Einsnorm des Differenzvektors und ist – vereinfacht ausgedrückt – die Summe aller Änderungen der Vermögensanlagen ohne Berücksichtigung des Vorzeichens.
bildet die sogenannte Einsnorm des Differenzvektors und ist – vereinfacht ausgedrückt – die Summe aller Änderungen der Vermögensanlagen ohne Berücksichtigung des Vorzeichens.
Mit ![]() ist somit dasjenige Volumen bezeichnet, dass in etwa pro Teilschritt (Einzeldrehung) umgesetzt wird. Die Anzahl der Teilschritte
ist somit dasjenige Volumen bezeichnet, dass in etwa pro Teilschritt (Einzeldrehung) umgesetzt wird. Die Anzahl der Teilschritte ![]() sollte vom Portfoliomanager im Rahmen der Linearumsetzungsstrategie II so gewählt werden, dass eine Umschichtung des Volumens
sollte vom Portfoliomanager im Rahmen der Linearumsetzungsstrategie II so gewählt werden, dass eine Umschichtung des Volumens ![]() innerhalb des Teilschritts
innerhalb des Teilschritts ![]() marktschonend – also nicht den Preis verzerrend – erfolgen kann.
marktschonend – also nicht den Preis verzerrend – erfolgen kann.
Neben den Vorteilen der Linearumsetzungsstrategie I bietet die zweite Variante weitere Vorteile:
- Mit wenigen Startparametern ist sie in automatisierten Handelssystemen implementierbar.
- Das Umschichtungsvolumen von Teilschritt zu Teilschritt ist abhängig von der Lage der Gewichtsvektoren des Ausgangs- und Zielportfolios im Raum, damit ist die Systematik der Linearumsetzungsstrategie II für andere Marktteilnehmer schwer erkennbar.
- Die Linearumsetzungsstrategie II ist auch manuell in nicht zeitlich äquidistanten Teilschritten umsetzbar, so dass die Wahrscheinlichkeit eines Vorpositionierens anderer Markteilnehmer weiter deutlich reduziert werden kann.
Beispiel zur Linearumsetzungsstrategie II
Betrachtet wird das gleiche Beispiel wie bei der Linearumsetzungsstrategie I.
Ein Portfoliomanager verwaltet ein Portfolio mit einem Gesamtvolumen ![]() in Höhe von 5 Milliarden Euro.
in Höhe von 5 Milliarden Euro.
Es befinden sich nur drei verschiedene Vermögensanlage ![]() und
und ![]() mit der Ausgangsgewichtung von
mit der Ausgangsgewichtung von
![]()
in dem Portfolio.
Das Management hat festgelegt, dass alle Vermögensanlagen Anteile zwischen ![]() und
und ![]() annehmen können. Damit sind die untere und obere Begrenzung durch die Vektoren
annehmen können. Damit sind die untere und obere Begrenzung durch die Vektoren
![]()
bzw.
![]()
gegeben.
Eine Portfoliooptimierung führte zu dem Zielportfolio mit dem neuen Gewichtsvektor
![]() .
.
Während die Vermögensanlage ![]() gleich bleibt, wird eine 10% Umschichtung
gleich bleibt, wird eine 10% Umschichtung ![]() durchzuführen sein.
durchzuführen sein.
Das Gesamtumschichtungsvolumen beträgt also 500 Millionen Euro. Der Portfoliomanager entscheidet sich, die Umschichtung in ![]() Wochen umzusetzen, d.h. pro Woche werden rund 41,67 Millionen Euro umgeschichtet.
Wochen umzusetzen, d.h. pro Woche werden rund 41,67 Millionen Euro umgeschichtet.
Bestimmung der Drehmatrix
Einheitsvektoren in Richtung der gegebenen Gewichtsvektoren ![]() und
und ![]() :
:
![]()
Der Winkel zwischen den gegebenen Gewichtsvektoren wird mit den soeben errechneten Einheitsvektoren bestimmt:
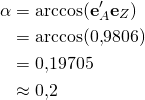
Bemerkung: Dieser Winkel entspricht etwa 11,3 Grad (![]() 360 Grad).
360 Grad).
Die Orthonormalbasis in der Drehebene wird mit Hilfe des Gram-Schmidtschen Orthogonalisierungsverfahrens aus den zuvor bestimmten Einheitsvektoren ermittelt:
![]()
Die Erzeugende der infinitesimalen Drehung ist dann die 3 ![]() 3 Matrix:
3 Matrix:
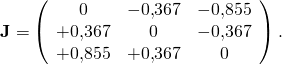
Mit ![]() und
und ![]() ist die Drehmatrix somit durch das Matrixexponential
ist die Drehmatrix somit durch das Matrixexponential ![]() gegeben:
gegeben:
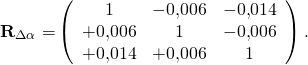
Diese Drehmatrix wird nun in die zentrale Gleichung der Linearumsetzungsstrategie II eingesetzt und der Gewichtsvektor ![]() des Ausgangsportfolios in
des Ausgangsportfolios in ![]() Teilschritten gedreht:
Teilschritten gedreht:
![]()
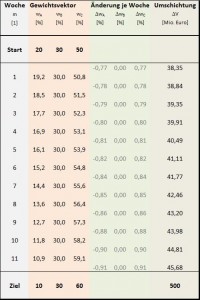
Die nachfolgende Tabelle zeigt die einzelnen Ergebnisse der Teilschritte im Überblick.
Die erste Spalte benennt die Teilschritte bzw. Einzeldrehungen. Hierbei bezeichnet „Start“ das Ausgangsportfolio und „Ziel“ das Zielportfolio. In diesem Beispiel finden insgesamt ![]() Einzeldrehungen statt.
Einzeldrehungen statt.
Die Spalten 2 bis 4 zeigen je Teilschritt die jeweiligen Gewichtungen der Vermögensanlagen ![]() und
und ![]()
In den Spalten 5 bis 7 sind die einzelnen Gewichtsveränderungen in dem entsprechenden Teilschritt notiert. Die letzte Spalte gibt an, wieviel Volumen in dem betrachteten Teilschritt umgeschichtet wird.
Das Beispiel zeigt, dass die Linearumsetzungsstrategie II dem Portfoliomanager von Woche zu Woche unterschiedliche Volumen zur Umschichtung empfiehlt. Die wöchentlichen Umschichtungsvolumen liegen in der zuvor berechneten Größenordnung von rund 41,67 Millionen Euro.
Bemerkung: Nehmen die ursprünglichen Gewichtsvektoren für Ausgangs- und Zielportfolio bei einer neuen Portfoliooptimierung andere Lagen im Raum ein, so ist zu beobachten, dass das Umschichtungsvolumen mal bei den ersten Einzeldrehungen, mal bei den letzten Einzeldrehungen oder zwischendurch am Größten ist. Diese Eigenschaft der Linearumsetzungsstrategie II erschwert es anderen Marktteilnehmer zusätzlich, die hier vorgestellte Systematik zu erkennen.