Tabellen für die kritischen Werte beim Kolmogorow-Smirnow-Test
Vielfältige Anwendungsbereiche in der Praxis erfordern die Anpassung von Verteilungsfunktionen an einen gegebenen Datensatz.
Die ermittelten Verteilungsfunktionen liefern dann statistische Größen zur Charakterisierung des Prozesses, dem die vorgelegten Daten entstammen.
Einfache Beispiele hierzu: Erwartungswert und Varianz.
Im Allgemeinen werden die statistischen Größen nicht nur für aktuelle Einschätzungen – bspw. dem momentanen Value-at-Risk einer Vermögensanlage, sondern auch für Prognosen genutzt, die sich auf künftige Berichtszeiträume beziehen.
Beispiel: Extremwertstatistik zur Risikobewertung im Portfoliomanagement.
Die Qualität der Charakterisierung des zugrundeliegenden Prozesses und der daraus abgeleiteten Aussagen hängt allerdings entscheidend von der Güte der Anpassung der Verteilungsfunktion an den gegebenen Datensatz ab.
D.h., in der Praxis wird zunächst die Güte der Anpassung der Verteilungsfunktion zu belegen sein, bevor auf weitere belastbare Ergebnisse geschlossen werden kann.
Beispiel: Modellierung operationeller Risiken
Hohe Anforderungen an die Methodik stellen der Gesetzgeber und die Aufsichtsbehörden z.B. bei der Anwendung des fortgeschrittenen Messansatzes (AMA: Advanced Measurement Approach) zur Bewertung operationeller Risiken in Finanzinstituten.
So ist zur Erteilung der Nutzungserlaubnis eines fortgeschrittenen Messansatzes u.a. die Angemessenheit des Messansatzes und dessen Überprüfung nachzuweisen und zu dokumentieren, vgl. auch Verordnung (EU) Nr. 575/2013 dort insbesondere Artikel 321 ff.
In der Konzeptionsphase neuer Ansätze liegen i.d.R. nur wenige Schadensmeldungen aufgrund operationeller Risikoereignisse aus vergangenen Berichtszeiträumen vor.
Oft umfasst die Datenbasis der Schadensmeldungen lediglich Quartals- oder Monatszahlen der letzten zwei Jahre, die zur Anpassung von Verteilungsfunktionen genutzt werden können.
Bei solch geringer Datenbasis ist die Schätzung der Verteilungsparameter häufig mit großen Unsicherheiten behaftet und eine losgelöste, etablierte Verfahrensüberprüfung z.B. mit Hilfe der Bestimmung der Anpassungsgüte dringend angezeigt.
Auch zur Vermeidung unnötiger Kosten durch Fehlentwicklungen – bspw. falsche Modellwahl, sollte der Nachweis und die Überprüfung der Güte institutsintern bereits im frühen Entwicklungsstadium erfolgen.
Hierzu stehen verschiedene, standardisierte Gütetests zur Verfügung, die in umfassenden, z.T. teuren Softwarepaketen bereits implementiert sind.
Auswahl an Beispielen für Gütetests:
- Chi-Quadrat-Test
- Cramér-von-Mises-Test
- Anderson-Darling-Test
- Kullback-Leibler-Divergenz
- Akaike-Informationskriterium
- Kolmogorow-Smirnow-Test
Gerade zu Beginn, wenn erste Ideen im Rahmen von Vorstudien zu neuen, fortgeschrittenen Messansätzen getestet werden sollen, stehen jedoch oft die benötigten Softwarepakete nicht zur Verfügung, um die Güte zu bestimmen. Hier sind einfache, möglichst in Excel realisierbare Lösungen wünschenswert.
Der Aufwand zur Umsetzung einiger der vorgenannten Gütetests in Excel ist allerdings hoch.
Es bietet sich aber mit dem Kolmogorow-Smirnow-Test auch eine einfache Möglichkeit in einer Excel-Tabelle eine schnelle Bestimmung der Güte durchzuführen.
Zur Bewertung der Güte sind dazu jedoch die kritischen Werte beim Kolmogorow-Smirnow-Test erforderlich und in der Excel-Tabelle zu hinterlegen.
Ist der Kolmogorow-Smirnow-Test in Excel abgebildet und sind die kritischen Werte hinterlegt, steht eine günstige Möglichkeit zur Verfügung eine Ersteinschätzung der Anwendbarkeit der Verteilungsfunktion des geplanten Messansatzes durchzuführen.
Wird das gesamte Testverfahren nachvollziehbar dokumentiert, kann die Dokumentation als Unterstützung zum Nachweis der Angemessenheit des Messansatzes genutzt werden.
Verallgemeinerung des Anwendungsfalls
Das vorgenannte Beispiel der Modellierung des operationellen Risikos ist exemplarisch für die allgemeine Situation am Anfang einer Neukonzeption.
Für den Fall, dass
- wenige Daten vorliegen,
- sich die Konzeption eines neuen Verfahrens noch in einem frühen Entwicklungsstadium befindet,
- kein umfangreiches Softwarepaket vorhanden ist, daher z.B. auf eine einfache Excel-Lösung zurückgegriffen werden soll,
- und ein einfacher Gütetest mit Hilfe des Kolmogorow-Smirnow-Test gewünscht ist,
stellen wir in diesem Beitrag exemplarisch für einige gängige Verteilungsfunktionen die kritischen Werte beim Kolmogorow-Smirnow-Test in Tabellenform zusammen.
Die kritischen Werte des Kolmogorow-Smirnow-Test: Tabellen
Beliebige bekannte, nicht angepasste Verteilung:
Exponentialverteilung:
Normal-Verteilung:
Gumbel-Verteilung:
Die kritischen Werte beim Kolmogorow-Smirnow-Test: Literatur
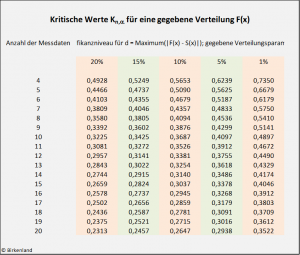
Beliebige bekannte, nicht angepasste Verteilung
Die kritischen Werte beim Kolmogorow-Smirnow-Test für eine beliebige nicht angepasste Verteilung: Tabelle.
Näherungsformeln für verschiedene angepasste Verteilungen
Shorack et al. stellen Grenzwerte (Percentage Points of Statistic 
) und Näherungsformeln zur Verfügung, mit deren Hilfe die benötigten kritischen Werte für verschiedene angepasste Verteilungen in sehr guter Approximation berechnet werden können.
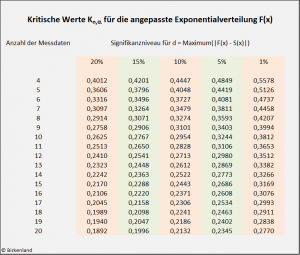
Exponentialverteilung
Lilliefors hat 1969 die kritischen Werte für den Kolmogorow-Smirnow-Test bei der angepassten Exponentialverteilung angegeben.
Die kritischen Werte beim Kolmogorow-Smirnow-Test für die Exponentialverteilung: Dokumentation der Berechnung.
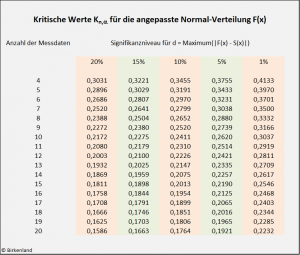
Normal-Verteilung
Lilliefors hat 1967 die kritischen Werte für den Kolmogorow-Smirnow-Test bei der angepassten Normal-Verteilung angegeben.
Die kritischen Werte beim Kolmogorow-Smirnow-Test für die Normal-Verteilung: Dokumentation der Berechnung.
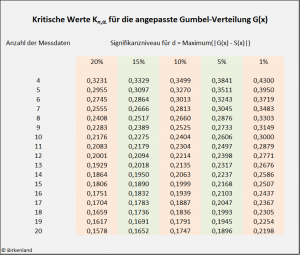
Gumbel-Verteilung
Chandra et al. hat 1981 die kritischen Werte für den Kolmogorow-Smirnow-Test bei der angepassten Gumbel-Verteilung angegeben.
Die kritischen Werte beim Kolmogorow-Smirnow-Test für die Gumbel-Verteilung: Dokumentation der Berechnung.